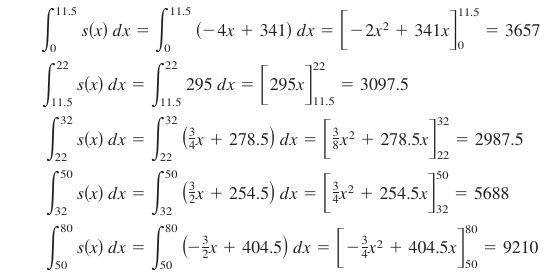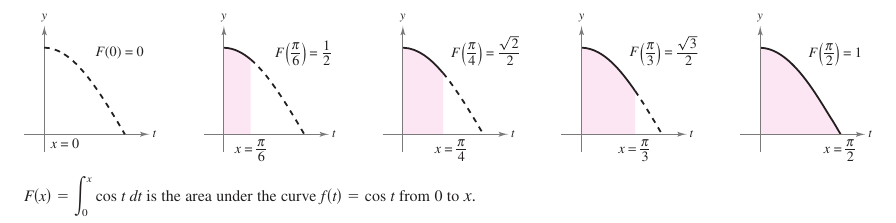Calculus I 04.04 The Fundamental Theorem of Calculus
| Previous | Calculus I 04.03 Riemann Sums and Definite Integrals |
| Next | Calculus I 04.05 Integration by Substitution |
Contents
4.4 The Fundamental Theorem of Calculus
- The Fundamental Theorem of Calculus.
- The Mean Value Theorem for Integrals.
- Find the average value for a function over a closed interval.
- The Second Fundamental Theorem of Calculus.
- The Net Change Theorem.
The Fundamental Theorem of Calculus
The discussion has covered two major calculus branches, differential calculus, the from tangent line problem, and integral calculus, from the area problem. These two problems might seem unrelated, but they are closely related. The connection was discovered independently by Isaac Newton[1] and Gottfried Leibniz[2] and is stated in the Fundamental Theorem of Calculus.
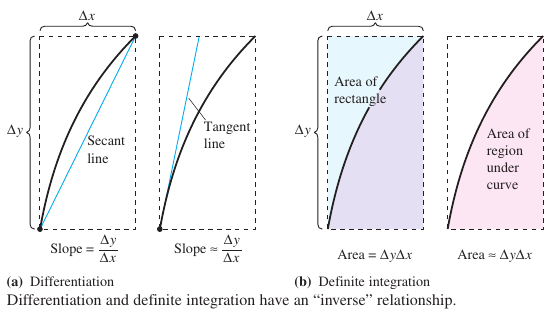
Simply, the theorem states that differentiation and definite integration are inverse operations, in the same sense that division and multiplication are inverse operations. To see how Newton and Leibniz might have anticipated this relationship, consider the approximations shown in Figure 4.4.1. The slope for the tangent line was defined using the quotient \(\Delta y/ \Delta x\), the slope for the secant line. Similarly, the area for a region under a curve was defined using the product \(\Delta y \Delta x\), the area for a rectangle. At least in the primitive approximation stage, the operations for differentiation and definite integration show an apparent inverse relationship in the same sense that division and multiplication are inverse operations. The Fundamental Theorem of Calculus states that the limit processes, used to define the derivative and definite integral, preserve this inverse relationship.
Theorem 4.4.1 The Fundamental Theorem of Calculus
If a function \(f\) is continuous on the closed interval \([a,b]\) and \(F\) is an antiderivative for \(f\) on the same interval, then
- $$\int_{a}^{b} f(x)\:dx= F(b)-F(a).$$
Proof The key to this proof is writing the difference \(F(b)-F(a)\) in a convenient form. Let \(\Delta\) be any partition for \([a,b]\).
- \(a=x_0< x_1<x_2< \cdot \cdot \cdot< x_{n-1}\)
By pairwise subtraction and addition with like terms, it can be expressed as
- \(F(b)-F(a)= F(x_n) - F(x_{n-1})+F(x_{n-1}- \cdot \cdot \cdot - F(x_1)+F(x_1)-F(x_0)\)
By the Mean Value Theorem there exists a number \(c_i\) in the \(i\)th subinterval such that
- $${F}'(c_i)=\frac{F(x_i)-F(x_{i-1})}{x_i-x_{i-1}}.$$
Because \({F}'(c_i)=f(c_i)\), let \(\Delta x_i=x_i-x_{i-1}\) and obtain
- $$F(b)-F(a)=\sum_{i=1}^{n} f(c_i) \Delta x$$
This important equation implies that by repeatedly applying the Mean Value Theorem created related \(c_i\)'s such that the constant \(F(b)-F(a)\) is a Riemann sum for for \(f\) on \([a,b]\) for any partition. Theorem 4.3.1 guarantees that the limit for Riemann sums over the partition with \(\left \| \Delta \right \|\to 0\) exists. Taking the limit, as \(\left \| \Delta \right \|\to 0\) produces
- $$F(b)-F(a) =\int_{a}^{b} f(x)\:dx.$$
Guidelines for using the Fundamental Theorem of Calculus
1. Provided an antiderivative exists and can be found for \(f\) there is a way to evaluate a definite integral without having to use the limit for a sum.
2. When applying the Fundamental Theorem of Calculus, use the notation below.
- $$\int_{a}^{b} f(x) \: dx= \left. F(x) \right ]_{a}^{b} = F(b)-F(a)$$
For example, to evaluate
- $$\int_{1}^{3} x^3 \: dx,$$
can be expressed as
- $$\int_{1}^{3} x^3\: dx = \left . \frac{x^4}{4} \right ]_{1}^{3} = \frac{3^4}{4} -\frac{1^4}{4}=\frac{81}{4}-\frac{1}{4}=20.$$
3. It is not necessary to include a constant \(C\) when evaluating the antiderivative
- $$\int_{a}^{b} f(x)\: dx =\left [ F(x)+C \right ]_{a}^{b} = [F(b)+C]=F(b)-F(a)$$
Example 4.4.1 Evaluating a Definite Integral
Evaluate each definite integral.
- $$\textbf{a.}\:\: \int_{1}^{2} (x^2-3)\:dx\:\:\:\: \textbf{b.}\:\: \int_{1}^{4} 3\sqrt{x}\:dx\:\:\:\:\textbf{c.}\:\: \int_{0}^{\pi /4} \sec^2 x\:dx$$
Solution
- $$\textbf{a.}\:\: \int_{1}^{2} (x^2-3)\:dx=\left [ \frac{x^3}{3}-3x \right ]_{1}^{2}= \left ( \frac{8}{3}-6 \right )- \left ( \frac{1}{3}-3 \right )= -\frac{2}{3}$$
- $$\textbf{b.}\:\: \int_{1}^{4} 3\sqrt{x}\:dx=3 \int_{1}^{4} x^{1/2}\:dx=3 \left [ \frac{x^{3/2}}{3/2} \right ]_{1}^{4}= 2(4)^{3/2}-2(1)^{3/2}=14$$
- $$\textbf{c.}\:\: \int_{0}^{\pi /4} \sec^2 x\:dx = \left. \tan x \vphantom{ \frac{3}{4} } \right ]_{0}^{\pi/4}= 1-0=1$$
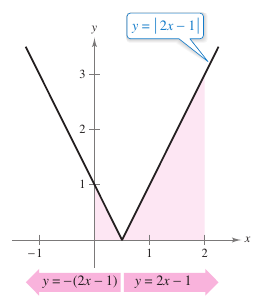
Example 4.4.2 A Definite Integral Involving Absolute Value
|
|
Evaluate
Solution Using Figure 4.4.2 and the definition for absolute value, rewrite the integrand as shown.
From this rewrite the integral in two parts.
|
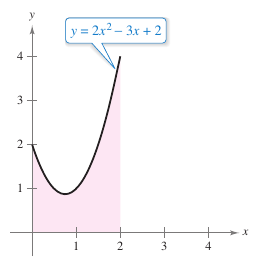
Example 4.4.3 Using the Fundamental Theorem to Find Area
|
|
Find the area for the region bounded by the graph for
the \(x\)-axis, and the vertical lines \(x=0\) and \(x=2\), as shown in Figure 4.3.3
|
The Mean Value Theorem for Integrals
|
|
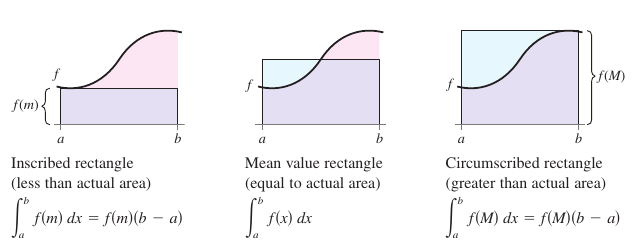
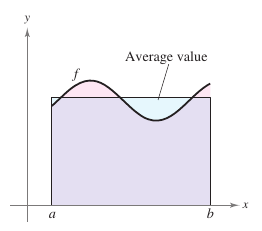
Section 4.2 showed the region's area under a curve is greater than the area for an inscribed rectangle and less than the area for a circumscribed rectangle. The Mean Value Theorem for Integrals states that somewhere “between” the inscribed and circumscribed rectangles, there is a rectangle whose area is precisely equal to the region's area under the curve, as shown in Figure 4.4.4. Theorem 4.4.2 Mean Value Theorem for IntegralsIf \(f\) is continuous on the closed interval \([a,b]\), then there exists a number \(c\)in the closed interval \([a,b]\) such that
Proof
for all \(x\) in \([a,b]\), apply Theorem 4.3.5 to write the following
From the third inequality apply the Intermediate Value Theorem to conclude that there exists some \(c\) in \([a,b]\) such that
|
Average Value for a Function
|
|
The value \(f(c)\) given in the Mean Value Theorem for Integrals is called the average value for \(f\) on the interval \([a,b]\). Definition 4.4.1 The Average Value for a Function on an IntervalIf \(f\) is integrable on the closed interval \([a,b]\), then the average value for (f\) on the interval is
To see why the average value for \(f\) is defined in this way, partition \([a,b]\) into \(n\) subintervals with equal width
If \(c_i\) is any point in the \(i\)th subinterval, then the arithmetic average, or mean, for \(f\)-values at the \(c_i\)'s is
Taking the limit as \(n \to \infty\) produces the average value for \(f\) on the interval \([a,b]\), as given in the Definition 4.4.1 above. Notice the region's area under the \(f\)'s graph is equal to the rectangle's area whose height is the average value, as shown in Figure 4.4.6. |
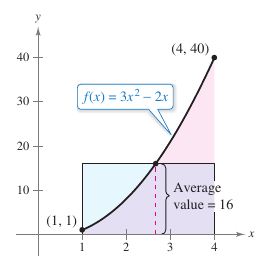
Example 4.4.4 Finding the Average Value for a Function
|
|
Find the average value for
on the interval \([1,4]\), as shown in Figure 4.4.7.
|
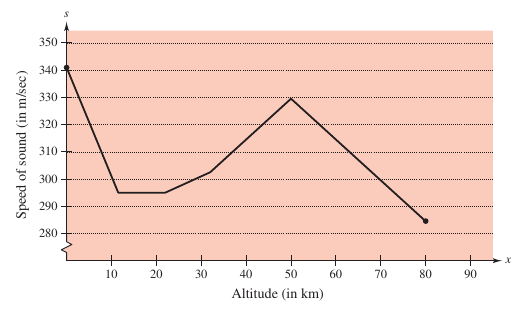
Example 4.4.5 The Speed of Sound
At different altitudes sound travels at different speeds. The speed of sound \(s(x)\), in meters per second, can be modeled by.
- $$s(x)=\left\{\begin{matrix}-4x+341, & 0 \leq x \leq 11.5 \\ 295, & 11.5 \leq x \leq 22\\ \frac{3}{4}+278.5, & 22 \leq x \leq 32 \\ \frac{3}{2x+}x+254.5 & 32 \leq x \leq 50 \\ - \frac{3}{2}+404.5 & 50 \leq x \leq 80 \end{matrix}\right.$$
where \(x\) is the altitude in kilometers, as shown in Figure 4.4.8. What is the average speed of sound over the interval \([0,80]\)?
Solution Begin by integrating \(s(x)\) over the interval \([0,80]\). Break the integral into five parts.
Adding the values for all five integrals produces
- $$\int_{0}^{80} s(x) \:dx=24,640.$$
The average speed of sound from the ground to 80 kilometers in altitude is
- $$\text{Average speed}=\frac{1}{80}\int_{0}^{80} s(x) \:dx=\frac{24,640}{80}=308\:\text{meters per second}.$$
The Second Fundamental Theorem of Calculus
Earlier, the definite integral for \(f\) on the interval \([a,b]\) was defined using the constant \(b\) as the integration's upper limit and \(x\) as the integration variable. However, a slightly different situation may arise in which the variable \(x\) is used as the integration's upper limit. To avoid the confusion in using \(x\) in two different ways, \(t\) is temporarily used as the integration variable. Remember that the definite integral is not a function of its integration variable.
Example 4.4.6 The Definite Integral as a Function
Evaluate the function
- $$F(x)=\int_{0}^{x} \cos t\: dt$$
at \(x=0,\:\frac{\pi}{6},\:\frac{\pi}{4},\:\frac{\pi}{3},\:\text{and}\:\frac{\pi}{2}.\)
Solution Evaluating all five different definite integrals is long and tedious. A simpler method is fixing \(x\) as a constant temporarily to produce
|
$$= \left. \vphantom{ \frac{3}{4} } \sin t \right ]_{0}^{x}$$ |
|
\(= \sin x - \sin 0\) | |
|
\(=\sin x\) |
Using \(F(x)=\sin x\) produces the results shown in Figure 4.4.9.
The function \(F(x)\) is accumulating the area under the curve \(f(t)= \cos t\) from \(t=0\) to \(t=x\). For \(x=0\), the area is zero and \(F(0)=0\). For \(x=\pi/2\), \(F(\pi/2)=1\) gives the accumulated area under the cosine curve on the entire interval \([0,\pi]\). This integral interpretation as an accumulation function is used often in integration applications.
Note the derivative for \(F\)is the original integrand, with only the variable changed, as illustrated in Example 4.4.6. That is,
- $$\frac{d}{dx} [F(x)]=\frac{d}{dx}[\sin x]=\frac{d}{dx} \left [ \int_{0}^{x} \cos t\:dt \right ]= \cos x.$$
This result is generalized in the Theorem 4.4.3, called the Second Fundamental Theorem of Calculus.
Theorem 4.4.3 The Second Fundamental Theorem of Calculus
If \(f\) is continuous on an open interval \(I\) containing \(a\), then, for every \(x\) in the interval,
- $$\frac{d}{dx} \left [ \int_{a}^{x} f(t)\:dt \right ]=f(x).$$
Proof Begin by defining \(F\) as
- $$F(x)=\int_{0}^{x} f(t) \:dt.$$
By the definition for the derivative, the equation is expressed as
|
$$=\lim_{\Delta x \to 0} \frac{F(x+\Delta x)-F(x)}{\Delta x}$$ |
|
$$=\lim_{\Delta x \to 0} \frac{1}{\Delta x} \left [ \int_{a}^{x+\Delta x} f(t)\:dt - \int_{a}^{x} f(t)\:dt \right ]$$ | |
|
$$=\lim_{\Delta x \to 0} \frac{1}{\Delta x} \left [ \int_{a}^{x+\Delta x} f(t)\:dt + \int_{x}^{a} f(t)\:dt \right ]$$ | |
|
$$=\lim_{\Delta x \to 0} \frac{1}{\Delta x} \left [ \int_{x}^{x+\Delta x} f(t)\:dt \right ].$$ |
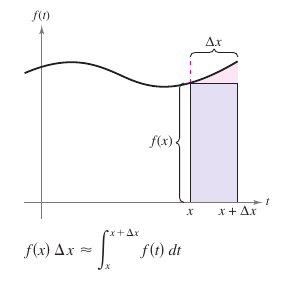
From the Mean Value Theorem for Integrals, assuming \(\Delta x > 0\), there exists a number \(c\) in the interval \([x, x+\Delta x]\) such that the integral in the expression above is equal to \(f(x)\Delta x\). Moreover, because \(x \leq c \leq x+\Delta x\), it follows that \(c \to x\) as \(\Delta x \to 0\). This produces
- $${F}'(x)=\lim_{\Delta x \to 0} \left [ \frac{1}{\Delta x} f(c) \Delta x \right ]= \lim_{\Delta x \to 0} f(c)=f(x).$$
A similar argument can be made for \(\Delta x < 0\).
|
|
Using the area model for definite integrals, the approximation
can be viewed as saying that the rectangle's area with height \(f(x)\) and width \(\Delta x\) is approximately equal to the region's area lying between the graph for \(f\) and the \(x\)-axis on the interval
as shown in Figure 4.4.10. Note the Second Fundamental Theorem of Calculus states that when a function is continuous, it has an antiderivative. This antiderivative need not, however, be an elementary function. |
Example 4.4.7 The Second Fundamental Theorem of Calculus with a Square Root
Evaluate
- $$\frac{d}{dx} \left [ \int_{0}^{x} \sqrt{t^2+1}\:dt \right ].$$
Solution Note that \(f(t)=\sqrt{t^2+1}\) is continuous on the entire real number line. Using the Second Fundamental Theorem of Calculus the expression can be written as
- $$\frac{d}{dx} \left [ \int_{0}^{x} \sqrt{t^2+1}\:dt \right ]=\sqrt{x^2+1}.$$
The differentiation shown in Example 4.4.7 is a straightforward application using the Second Fundamental Theorem of Calculus. Example 4.4.8 shows how this theorem can be combined with the Chain Rule to find the derivative for a function.
Example 4.4.8 The Second Fundamental Theorem of Calculus with the Chain Rule
Find the derivative for
- $$F(x)=\int_{\pi/2}^{x^3} \cos t\:dt.$$
Solution Let \(u=x^3\) and apply the Second Fundamental Theorem of Calculus with the Chain Rule to produce,
|
$$=\frac{dF}{du} \frac{du}{dx}$$ |
Chain Rule |
|
$$=\frac{d}{du}[F(x)]\frac{du}{dx}$$ |
Definition for \(\frac{dF}{fu}\) | |
|
$$=\frac{d}{du} \left [ \color{red}{\int_{\pi/2}^{x^3} \cos t\:dt} \right ]\frac{du}{dx}$$ |
Substitute \(\int_{\pi/2}^{x^3} \cos t\:dt\) for \(F(x)\). | |
|
$$=\frac{d}{du} \left [ \int_{\pi/2}^{\color{red}{u}} \cos t\:dt \right ]\frac{du}{dx}$$ |
Substitute \(u\) for \(x^3\). | |
|
\(=(\cos u)(3x^2)\) |
Apply Second Fundamental Theorem of Calculus | |
|
\(=(\cos x^3)(3x^2)\) |
Substitute \(x^3\) for \(u\).
|
Because the integral in Example 4.4.8 is easily integrated, verify the derivative as follows.
|
$$=\int_{\pi/2}^{x^3} \cos t\:dt$$ |
|
$$= \left. \vphantom{ \frac{3}{4}} \sin t \right ]_{\pi/2}^{x^3}$$ | |
|
\(=\sin x^3 - \sin \frac{\pi}{2}\) | |
|
\(= \sin x^3-1\) |
With the equation in this form apply the Power Rule to verify the derivative for \(F\) is the same as obtained in Example 4.4.8.
|
Derivative for \(F\) |
Net Change Theorem
The Fundamental Theorem of Calculus states that if \(f\) is continuous on the closed interval \([a,b]\) and \(F\) is an antiderivative for \(f\) on \([a,b]\), then
- $$\int_{a}^{b} f(t)\:dx=F(b)-F(a).$$
But because \({F}'=f(x)\), this statement can rewritten as
- $$\int_{a}^{b} {F}'(x)\:dt=F(b)-F(a).$$
where the quantity \(F(b)-F(a)\) represents the net change for \(F\) on the interval \([a,b]\).
Theorem 4.4.4 The Net Change Theorem
The definite integral for the change rate for quantity \({F}'(x)\) gives the total change, or net change, in that quantity on the interval \([a,b]\).
|
Net change for \(F\) |
Example 4.4.9 Using the Net Change Theorem
A chemical flows into a storage tank at \((180+3t)\) liters per minute, where \(t\) is the time in minutes and \(0 \leq t \leq 60\). Find how chemical much flows into the tank during the first 20 minutes.
Solution Let \(c(t)\) be the how much chemical is in the tank at time \(t\). Then \({c}'(t)\) represents the rate at which the chemical flows into the tank at time \(t\). During the first 20 minutes, the amount that flows into the tank is
|
$$=\int_{0}^{20} (180+3t)\:dt$$ |
|
$$= \left [ 180t+\frac{3}{2}t^2 \right ]_{0}^{20}$$ | |
|
\(=3600+600\) | |
|
\(=4200.\) |
The amount flowing into the tank during the first 20 minutes is 4200 liters.
Another way to illustrate the Net Change Theorem is by examining a particle's velocity moving along a straight line, where \(s(t)\) is the position at time \(t\). Then its velocity is \(v(t)={s}'(t)\) and
- $$\int_{a}^{b} v(t)\:dt=s(b)-s(a).$$
This definite integral represents the net change in position, or displacement, for the particle.
|
|
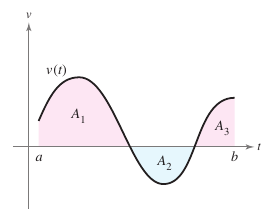
When calculating the total distance traveled by the particle, consider the intervals where \(v(t) \leq 0\) and the intervals where \(v(t) \geq 0\). When \(v(t) \leq 0\), the particle moves to the left, and when \(v(t) \geq 0\), the particle moves to the right. Calculate the total distance traveled by integrating the velocity's absolute \(\left | v(t)) \right |\). The particle's displacement on the interval \([a,b]\) is
and the total distance traveled by the particle on \([a,b]\) is
as shown in Figure 4.4.11. |
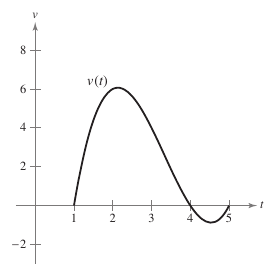
Example 4.4.10 Solving a Particle Motion Problem
|
|
The velocity for a particle in feet per second moving along a line is
where \(t\) is time in seconds.
The particle move \(\frac{32}{3}\) feet to the right.
| ||||||||||||||||||||||||||||||||||||
Internal Links
Parent Article: Calculus I 04 Integration