Calculus II 07.05 Work

Previous	Calculus II 07.04 Arc Length and Surfaces for Revolution
Next	Calculus II 07.06 Moments Centers of Mass and Centroids

7.5 Work

• Find the work done by a constant force.
• Find the work done by a variable force.

Work Done by a Constant Force

Work, as used in the sciences and engineering disciplines, is the energy needed to perform various mechanical jobs. For example, how much work is needed when a crane lifts a steel girder, when a spring is compressed, when a rocket is propelled into the air, or when a truck pulls a load along a highway, is essential in calculating how much energy is needed for the job. In general, work is done by a force when it moves an object. If the force applied to the object is constant, then the definition for work is defined below.

Definition 7.5.1 Work Done by a Constant Force

If an object is moved a distance \(D\) in a direction by applying a constant force \(F\), then the work \(W\) done by the force is defined as \(W = FD\).

Force has four fundamental types: gravitational, electromagnetic, strong nuclear, and weak nuclear. A force pushes or pulls on an object. For gravity using an object's weight, not mass, is common for measurement.

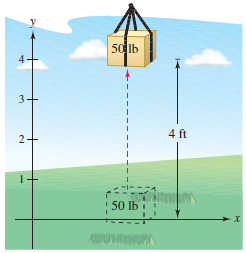
Example 7.5.1 Lifting an Object

The work done in lifting a 50-pound object 4 feet is 200 foot-pounds. Figure 7.5.1

Determine the work done in lifting a 50-pound object 4 feet above the ground. Solution The force \(F\) is the object's weight, as shown in Figure 7.5.1. The work done in lifting the object 4 feet is \(W\) \( = FD \) Work = (force)(distance) \( = 50(4) \) Force = 50 pounds, distance = 4 feet \( = 200\:\: \text{foot-pounds} \)

Work Done by a Variable Force

The force changes as an object changes position \(\Delta x\). Figure 7.5.2

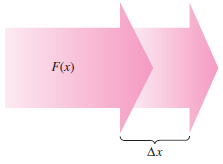
In Example 7.5.1, the force was constant, as in unchanging over time and distance. When a variable force is applied to an object, calculus is needed to determine the work done, because the force applied to the object changes strength over time and distance. For instance, the force required to compress a spring increases as the spring is compressed. Consider an object that is moved along a straight line from \(x=a\) to \(x=b\) by a continuously varying force \(F(x)\). Let \(\Delta\) be a partition that divides the interval \([ a,b ]\) into subintervals \(n\) determined by $$a=x_{0} < x_{1} < x_{2} < \cdots < x_{n} =b $$ and let \(\Delta x_{i}=x_{i}-x_{i-1}\). For each \(i\), choose a \(c_{i}\) such that $$ x_{i-1} \leq c_{i} \leq x_{i} .$$ Then at \(c_{i}\) the force is \(F(c_{i})\). Because \(F\) is continuous, you can approximate the work done in moving the object through the \(i\)th subinterval by the increment $$\Delta W_{i} = F(c_{i}) \Delta x_{i} .$$ as shown in Figure 7.5.2. The total work done as the object moves from \(a\) to \(b\) is approximated by $$W \approx \sum_{i=1}^{n} \Delta W_{i} $$ This approximation improves as \( \| \Delta \| \rightarrow 0 (n \to \infty ) \). The work done sums to \(W\) $$ = lim_{\| \Delta \| \rightarrow 0 } \sum_{i=1}^{n} F(c_{i}) \Delta x_{i} $$ $$ = \int_{a}^{b} F(x)\: dx $$

Definition 7.5.2 Work Done by a Variable Force

If an object is moved along a straight line by a continuously varying force \( F(x) \), then the work \(W\) done by the force as the object is moved from

$$x=a \text{ to }x=b $$

is given by

$$W$$	$$ = \lim_{ \| \Delta \| \rightarrow 0 } \sum_{i=1}^{n} \Delta W_{i} $$
	$$ = \int_{a}^{b} F(x)\: dx $$

Where distance \(x\) is incremented

$$ \Delta W = (force)(distance \: increment) = (F) \left( \Delta x \right).$$

Where force \(x\) is incremented, but distance is constant

$$ \Delta W = (force \: increment)(distance) = (\Delta F)(x)$$

is useful in movement problems involving nonrigid objects like chains, fluids and gases.
Other problems increment both

$$ \Delta W = (force \: increment)(distance \: increment) = (\Delta F)(\Delta x).$$

Example 7.5.2 Hook's Law: Compressing a Spring

Figure 7.5.3

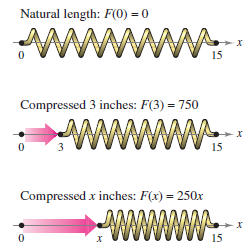
Hooke’s Law[1]: The force \(F\) required to compress or stretch a spring (within its elastic limits) is proportional to the distance \(d\) that the spring is compressed or stretched from its original length. As an equation, $$F=kd$$ where the proportionality constant \(k\) (the spring constant) depends on the spring's specific properties. A 750 pound force compresses a spring 3 inches from its normal 15 inch length. Calculate the work done in compressing the spring an additional 3 inches. Solution By Hooke's Law, the force \(F(x)\) required to compress the spring \(x\) units from its normal length is \(F(x)=kx\). Because \(F(3)=750\) the formula breaks down as $$F(x)=(k)(3) \rightarrow 750=3k \rightarrow 250=k$$ Figure 7.5.3 shows that \(F(x)= 250\). To find the work increment assume that the force required to compress the spring over any small increment \(\Delta x\) is constant to an acceptable tolerance. The formula for each work increment is $$\Delta W=(force)(distance \: increment) = (250x) \Delta x.$$ Because the spring is compressed from \( x=0\) to \(x=6\) inches less than its normal length, the work required is $$W= \int_{a}^{b} F(x)\:dx = \int_{3}^{6} 250x \: dx = 125x^{2} \bigg]_{3}^{6} = 4500 - 1125 = 3375 \text{ inch-pounds.}$$ Note that integration is not integrate from \(x=0\) to \(x=6\) because the work done in compressing the spring an additional 3 inches (not including the first 3 inches).

Example 7.5.3 Newton's Universal Gravitation Law: Launching a Spacecraft into Orbit

Figure 7.5.4

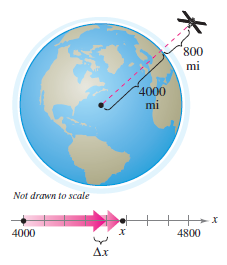
Newton’s Universal Gravitation Law[2]: The attractive force \(f\) between to bodies with masses \(m_{1}\) and \(m_{2}\) is proportional to their product and inversely proportional to the distance \(d\) squared d between the bodies. As a formula $$F=G\frac{m_{1}m_{2}}{d^{2}} $$ When \(m_{1}\) and \(m_{2}\) are measured in kilograms and d in meters, \(F\) will be in newtons with the value \(G= 6.67 \: \text{x} \: 10^{-11}\) cubic meter per kilogram-second squared, where \(G\) is the Gravitational Constant. A spacecraft weighs 15 metric tons on Earth's surface. How much work is done in propelling it to an 800 mile altitude, as shown in Figure 7.5.4? (Use 4000 miles as the Earth's radius. Do not consider air resistance or fuel weight.) Solution Because the spacecraft weight varies inversely as the squared distance from the Earth's center, the force \(F(x)\) exerted by gravity is $$F(x)=\frac{C}{x^{2}}$$ where \(C\) is the constant of proportionality. Because the spacecraft weighs 15 metric tons on Earth's surface and Earth's radius is approximately 4000 miles, this produces $$ 15 = \frac{C}{(4000)^{2}} \rightarrow 240,000,000 = C.$$ The work increment is $$ \Delta W = (force)(distance \: increment) = \frac{240,000,000}{x^{2}} \Delta x.$$ Because the spacecraft is propelled from \(x=4000\) to \(x=4800\) miles, the total work done is $$W$$ $$ = \int_{a}^{b} F(x)\: dx $$ Formula for work $$ = \int_{4000}^{4800} \frac{240,000,000}{x^{2}} \: dx $$ Substitute variables $$ = \frac{-240,000,000}{x} \Bigg]_{4000}^{4800} $$ Integrate \( = -50,000 + 60,000 \) \( = 10,000 \text{ mile-tons }\approx 1.164 \times 10^{11} \text{ foot-pounds. } \) In SI units, using 1 foot-pound \( \approx 1.35582\) joules, the work done is \( W \approx 1.578 \: \text{x} \: 10^{11}\) joules.

Example 7.5.4 Emptying an Oil Tank

Figure 7.5.5

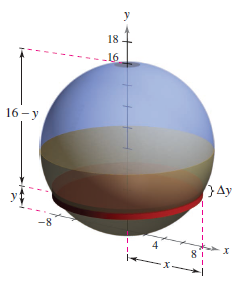
The spherical tank in Figure 7.5.5 has an 8 foot radius and is half filled with oil that weighs 50 pounds per cubic foot. Find the work required to pump the oil out through a hole in the top. Solution Divide the oil into disks with thickness \(\Delta y\) and radius \(x\) as shown in Figure 7.5.5. Because the incremental force for each disk is given by its weight, the formula produced is \( \Delta F\) \( = weight \) $$= \left( \frac{50\:pounds}{cubic\:foot} \right)(volume) $$ $$= 50 \left( \pi x^{2} \Delta y \right) \:pounds. $$ For a circle with radius 8 feet and center at (0,8), produces \( \Delta F\) \( = 50 \left( \pi x^{2} \Delta y \right) \) \( = 50 \pi \left( 16y-y^{2} \right) \Delta y \). Notice any disk \(y\) feet from the bottom must be moved \((16-y)\) feet. The incremental work formula is \( \Delta W\) \( = \Delta F(16-y) \) \( = 50 \pi (16y-y^{2}) \Delta y(16-y) \) \( = 50 \pi (256y-32y^{2} + y^{3}) \Delta y \). Because the is half full, \(y\) ranges from 0 to 8, and the work required to empty the tank is \( W\) $$ = \int_{0}^{8} 50 \pi \left( 256y-32y^{2} + y^{3} \right) dy $$ $$ = 50 \pi \left[ 128y^{2}-\frac{32}{3}y^{2}+\frac{y^{4}}{4} \right]_{0}^{8} $$ $$ = 50 \pi \left( \frac{11,264}{3} \right)\approx 589,782 \text{ foot-pounds.} $$

Example 7.5.5 Lifting a Chain

Work required to raise a chain by one end. Figure 7.5.6

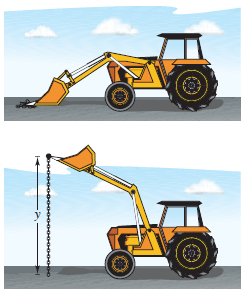
A 20-foot chain weighing 5 pounds per foot is lying coiled on the ground. How much work is required to raise one end 20 feet so that it is fully extended, as shown in Figure 7.5.6? Solution Divide the chain into small sections \(\Delta y\) long. The weight for each section is the incremental force $$\Delta F = (weight)= \left( \frac{5 pounds}{foot} \right)(length) = 5 \: \Delta y .$$ Because each section is raised to height y, the incremental formula is $$\Delta W = (force\:increment)(distance)=(5\Delta y)y = 5y \Delta y.$$ Because \(y\) ranges from 0 to 20, the total work is $$W = \int_{0}^{20} 5y\:dy = \frac{5y^{2}}{2} \Bigg]_{0}^{20} = \frac{5(400)}{2} = 1000 \text{ foot-pounds,} $$

Example 7.5.6 Coulomb's Law[3]: Sphere's with Negative Electric Charge

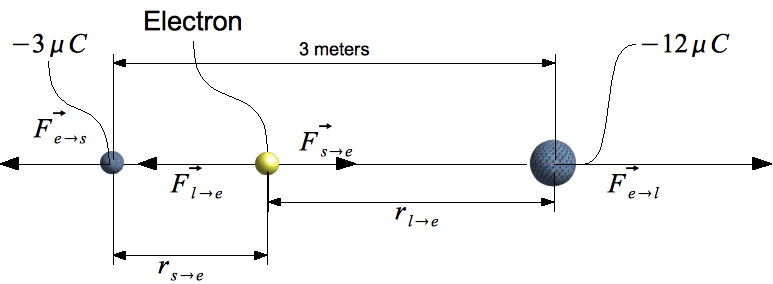
Two negatively charged spheres, \(-12 \mu C\) and \(-3 \mu C\), are 3 meters apart. Where could an electron be placed so that it will be suspended in space between them with a net zero force? Where do the negative charges cancel each other out? Ignore the repulsive force between the two charges because they are held in place. See Figure 7.5.7.
Solution In Figure 7.5.7 \(r_{s \rightarrow e} \) is the distance between the electron and the small charge, while \( \overrightarrow{F}_{s \rightarrow e} \) is the force the electron feels from it. To find the balancing point set the charges equal to each other and solve for a distance ratio.

$$\frac{kq_{s}q_{e}}{r_{s \rightarrow e}^{2}} $$	$$ = \frac{kq_{l}q_{e}}{r_{e \rightarrow l}^{2}} $$
$$ \frac{-3 \mu C}{r_{s \rightarrow e}^{2}} $$	$$ = \frac{-12 \mu C}{r_{e \rightarrow l}^{2}} $$
$$ \frac{r_{s \rightarrow e}^{2}}{r_{e \rightarrow l}^{2}} $$	$$ = \frac{-12 \mu C}{-3 \mu C} $$
$$ \frac{r_{s \rightarrow e}^{2}}{r_{e \rightarrow l}^{2}} $$	$$ = \sqrt{ \frac{1 \mu C}{4 \mu C}}= \frac{1}{2} $$

With this ratio we can place the electron 2 meters from the large charge and 1 meter from the small charge to find the perfect balance between them.

Figure 7.5.7

Example 7.5.7 Work Done by an Expanding Gas

Work Done by expanding gas Figure 7.5.8

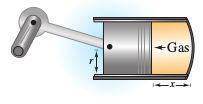
A cylinder and piston machine has enclosed a gas in a one cubic foot chamber at 500 pounds pressure per square foot. The gas expands to two cubic feet, thus pushing the piston back, as shown in Figure 7.5.8. Find the work done by the gas. (Assume that the pressure is inversely proportional to the volume.) Solution Let \(p\) represent the gas's pressure. Let \(r\) represent the cylinder's radius. Let \(x\) be the distance the piston is moved in feet. The work increment for moving the piston \(\Delta x\) feet is $$\Delta W = (force)(distance \: increment)=F( \Delta x ) = p \left( \pi r^{2} \right) \Delta x = p \Delta V.$$ As the gas volume expands from \(V_{0}\) to \(V_{1}\), the work done in moving the piston is $$W= \int_{V_{0}}^{V_{1}} p\: dV.$$ Assuming the gas pressure is inversely proportional to its volume produces $$p=\frac{k}{V}$$ the integral for work becomes $$W$$ $$ = \int_{V_{0}}^{V_{1}} \frac{k}{V} \: dV$$ $$=\int_{1}^{2} \frac{500}{V} \: dV$$     \(p=500\) when \(V=1\), then \(k=500\) $$=500 \ln |V| \Bigg]_{1}^{2} $$ $$ \approx 346.6 \text{ foot-pounds.}$$

Internal Links

Parent Article: Calculus II 07 Integration Applications