Calculus I 04.03 Riemann Sums and Definite Integrals
| Previous | Calculus I 04.02 Area |
| Next | Calculus I 04.04 The Fundamental Theorem of Calculus |
Contents
- 1 4.3 Riemann Sums and Definite Integrals
- 1.1 Riemann Sums[1]
- 1.2 Definite Integrals
- 1.3 Definite Integral Properties
- 1.3.1 Definition 4.3.3 Two Special Definite Integrals
- 1.3.2 Example 4.3.4 Evaluating Definite Integrals
- 1.3.3 Theorem 4.3.3 Definite Integral Properties
- 1.3.4 Example 4.3.6 Evaluating a Definite Integral
- 1.3.5 Theorem 4.3.4 Additive Interval Property
- 1.3.6 Example 4.3.5 Using the Additive Interval Property
- 1.3.7 Theorem 4.3.5 Preserving Inequality
- 2 Internal Links
4.3 Riemann Sums and Definite Integrals
- Evaluate Riemann Sums
- Evaluate Definite Integrals
Riemann Sums[1]
In Section 4.2 the partitions had equal width subintervals. This was done only for computational convenience. Partitions with even width subintervals are not always desirable or possible. Example 4.3.1 illustrates this.
Example 4.3.1 Evaluate a Partition with Unequal Subintervals Width
|
|
Consider the region bounded by the graph for
and the \(x\)-axis for \(0 \leq x \leq 1\), as shown in Figure 4.3.1. Evaluate the limit
where \(c_i\) is the right endpoint for the partition given by
and \(\Delta x_i\) is the width for the \(i\)th interval.
The limit is
|
|
|
Referring to Section 4.2, Example 4.2.7 the region shown in Figure 4.3.2's area is \(1/3\). Because the square bounded by \(0 \leq x \leq 1\) and \(0 \leq y \leq 1\) has the area 1, conclude the area for the region shown in Figure 4.3.2 has the area 2. This agrees with the limit found in Example 4.3.1, even though that example used a partition having subintervals with unequal widths. The reason this particular partition gave the proper area is that as \(n\) increases, the width for the largest subinterval approaches zero. This is a key feature for definite integrals. In Section 4.2, the limit for a sum was used to define the area for a region on a plane. This is only one means among many for evaluating a sum's limit. A similar approach is used to determine quantities as diverse as arc lengths, average values, centroids, volumes, work, and surface areas. The next definition is named after Georg Friedrich Bernhard Riemann.[2] Although the definite integral was developed long before Riemann’s time, he wrote the definitive description, allowing it's broad application. Definition 4.3.1 Riemann SumsLet \(f\) be defined on the closed interval \([a,b]\), and let \(\Delta\) be a partition for \([a,b]\) given by
where \(\Delta x\) is the width for the \(i\)th subinterval
If \(c_i\) is any point in the \(i\)th subinterval, then the sum
is called a Riemann Sum for \(f\) for the partition \(Delta\). Note that the function \(f\) has no restrictions other than being defined on the interval \([a,b]\). Section 4.2 used simplified Riemann sums, here they are described in more detail. |
The width for the largest subinterval on a partition \(\Delta\) is called the norm for the partition and is denoted by \(\left \| \Delta \right \|\). If every subinterval has equal width, then the partition is called regular and is denoted by
|
Regular partition |
For a general partition, the norm is related to how many subintervals \([a,b]\) is divided into, in the following way
|
General partition |
As the subinterval count on a partition approaches infinity, as the norm for the partition approaches 0. As an expression, \(\left \| \Delta \right \| \to 0\) implies that \(n \to \infty\).
The converse is not true. For example, let \(\Delta_n\) be the partition on the interval \([0,1]\) given by
- $$0 < \frac{1}{2^n} < \frac{1}{2^{n-1}} < \cdot \cdot \cdot < \frac{1}{8} < \frac{1}{4} < \frac{1}{2} < 1. $$
|
|
For any positive \(n\)-value, the norm for the partition is \(\Delta_{n}\) is \(1/2\), as shown in Figure 4.3.3. Letting \(n\) approach infinity does not force \(\left \| \Delta \right \|\) to approach 0. On a regular partition, however, the statements
are equivalent. |
Definite Integrals
To determine the definite integral, consider the limit
- $$\lim_{\left \| \Delta \right \| \to \infty} \sum_{i=1}^{n} f(c_i) \Delta x_i = L.$$
If this limit exists, then there exists a real number \(L\) such that for all \(\varepsilon >0\), there exists a \(\epsilon > 0 \) such that for every partition with \(\left \| \Delta \right \| < \delta\), it follows that
- $$ \left | L-\sum_{i=1}^{n} f(c_i) \Delta x_i \right | < \varepsilon $$
not matter what \(c_i\) is chosen on the \(i\)th subinterval for each partition \(\Delta\).
Definition 4.3.2 The Definite e Integral
If \(f\) is defined on the closed interval \([a,b]\) and the limit for Riemann sums over partition \(\Delta\)
- $$\lim_{\left \| \Delta \right \| \to \infty} \sum_{i=1}^{n} f(c_i) \Delta x_i$$
exists, then \(f\) is integrable on \([a,b]\) and the limit is denoted by
- $$\lim_{\left \| \Delta \right \| \to \infty} \sum_{i=1}^{n} f(c_i) \Delta x_i = \int_{a}^{b} f(x) dx.$$
The limit is called the definite integral for \(f\) from \(a\) to \(b\). The number \(a\) is integration's lower limit, and the number \(b\) is integration's upper limit.
Always remember that definite integrals and indefinite integrals are different concepts. A definite integral is a number, whereas an indefinite integral is many related functions. Though Riemann sums were defined for functions with very few restrictions, a sufficient condition for a function \(f\) to be integrable on \([a,b]\) is that it is continuous on \([a,b]\). A proof is beyond this text.
Theorem 4.3.1 Continuity Implies Integrability
If a function \(f\) is continuous on the closed interval \([a,b]\), then \(f\) integrable on \([a,b]\). That is,
- $$\int_{a}^{b} f(x) dx$$
does exist.
Example 4.3.2 Evaluating a Definite Integral as a Limit
|
|
Evaluate the definite integral
Solution The funtion \(f(x)=2x\) is integrable on the interval \([-2,1]\) because it is continuous on \([-2,1]\). The definition for integrability implies that any partition whose norm approaches 0 can be used to determine the limit. For computational convenience, define \(\Delta\) by subdividing the interval into \(n\) subintervals with equal width defined by
Choosing \(c_i\) as the right endpoint for each subinterval produces
The definite integral is
|
|
|
Because the definite integral in Example 4.3.2 is negative, it does not represent the area for the region shown in Figure 4.2.5. Definite integrals can be positive, negative, or zero. Interpenetrating a definite integral as an area, as defined in Section 4.2, the function \(f\) must be continuous and nonnegative on \([a,b]\), as stated in Theorem 4.3.2 below. Theorem 4.3.2 The Definite Integral as a Region's AreaIf \(f\) is continuous and nonnegative on the closed interval \([a,b]\), then the area for the region bounded by the graph for \(f\), the \(x\)-axis, and the vertical lines \(x=a\) and \(x=b\) is
as shown in Figure 4.3.5. |
|
|
To illustrate Theorem 4.3.2 consider the region bounded by the graph for
and the \(x\)-axis, as shown in Figure 4.3.6. Because \(f\) is continuous and nonnegative on the closed interval \([0,4]\), there area for the region is
A more straightforward technique for evaluating a definite integral like this will be discussed in Section 4.4. For this one, evaluate this definite integral in two ways, use the limit definition or check if the definite integral represents the area for a common geometric region, such as a rectangle, triangle, or semicircle. |
Example 4.3.3 Areas for Common Geometric Figures
Sketch the region corresponding to each definite integral. Then evaluate each integral using a geometric formula.
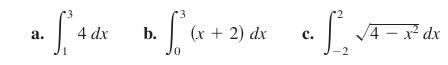
Solution A sketch for each region is shown in
a. This region is a rectangle with height 4 and width 2, as shown in Figure 4.3.7(a).
- $$\int_{1}^{3}4 dx=(\text{Rectangle area})=4(2)=8$$
b. This region is a trapezoid with an altitude 3 and parallel bases with lengths 2 and 5, as shown in Figure 4.3.7(b). The formula for a trapezoid's area is \(1/2h(b_1+b_2).\)
- $$\int_{0}^{3}(x+2) dx =(\text{Trapezoid area})=\frac{1}{2}(3)(2+5)=\frac{21}{2}$$
c. This region is a semicircle with radius 2. The formula for a semicircle's area is \(1/2 \pi r^2\).
- $$\int_{-2}^{2} \sqrt{4-x^2} dx =(\text{Trapezoid area})=\frac{1}{2}\pi (2^2)= 2\pi$$
The integration variable in a definite integral is sometimes called a dummy variable because it can be replaced by any other variable without changing the integral's value. For example, the definite integrals
- $$\int_{0}^{3}(x+2) dx \:\:\:\: \text{and} \:\:\:\: \int_{0}^{3} (t+2) dt$$
have the same value.
Definite Integral Properties
The definite integral definition for \(f\) on the interval \([a,b]\) specifies that \(a<b\). Now extend the definition to cover cases where \(a=b\) or \(a>b\). Geometrically, the next two definitions seem reasonable. For example, it makes sense to define a region's area with zero width and a finite height at zero.
Definition 4.3.3 Two Special Definite Integrals
- $$\:\textbf{1.}\:\: \text{If}\:f\: \text{is defined at }x=a,\: \text{then}\: \int_{a}^{a} f(x) dx =0.$$
- $$\:\textbf{2.}\:\: \text{If}\:f\: \text{is integrable on }[a,b], \: \text{then}\: \int_{b}^{a} f(x) dx =0.$$
Example 4.3.4 Evaluating Definite Integrals
Evaluate each definite integral.
- $$\textbf{a.} \int_{\pi}^{\pi} \sin x\: dx\:\:\:\:\textbf{b.} \int_{3}^{0} (x+2)\: dx$$
Solution
a. Because the sine function is defined at \(x=\pi\), and the upper and lower integration limits are equal, it can be expressed as
- $$\int_{\pi}^{\pi} \sin x \: dx=0.$$
b. This integral is the same as Example 4.3.3(b) except the upper and lower limits are exchanged. Because that has the value \(21/2\), it can be expressed as
- $$\int_{3}^{0} (x+2)\: dx=-\int_{0}^{3} (x+2)\: dx=-\frac{21}{2}.$$
|
|
In Figure 4.3.8, the larger region can be divided at \(x=c\) into two subregions whose intersection is a line segment. Because the line segment has zero area, it follows that the larger region's area is equal to the two smaller regions' summed area. |
Theorem 4.3.3 Definite Integral Properties
If \(f\) and \(g\) are integrable on \([a,b]\) and \(k\) is a constant, then the function \(kf\) and \(f\pm g\) are integrable on \([a,b]\), and
- $$\textbf{1.}\:\int_{a}^{b} kf(x)\: dx = k \int_{a}^{b} f(x)\:dx$$
- $$\textbf{2.}\:\int_{a}^{b} \left [f(x \pm g(x) \right ] = \int_{a}^{b} f(x)\:dx \pm \int_{a}^{b} g(x)\: dx$$
Property 2 extends to any finite number of functions.
Example 4.3.6 Evaluating a Definite Integral
Evaluate
- $$\textbf{1.}\:\int_{1}^{3} (-x^2+4x-3) \:dx$$
using all the following rules.
- $$\int_{1}^{3} x^2\:dx= \frac{26}{3},\:\:\:\:\int_{1}^{3} x \:dx,\:\:\:\:\int_{1}^{3}\:dx=2$$
Solution
|
$$=\int_{1}^{3} (-x^2) \:dx+\int_{1}^{3} 4x\: dx+\int_{1}^{3}(-3)\:dx$$ |
|
$$=-\int_{1}^{3} (-x^2) \:dx+4\int_{1}^{3} x\: dx-\int_{1}^{3}3\:dx$$ | |
|
$$=- \left ( \frac{26}{3}\right ) + 4(4) -3(2)$$ | |
|
$$=\frac{4}{3} |
Theorem 4.3.4 Additive Interval Property
If \(f\) is integrable on the three closed intervals determined by \(a,\:b,\:\text{and }c,\) then
- $$\int_{a}^{b}f(x) dx= \int_{a}^{c}f(x)dx+\int_{c}^{b}f(x)dx.$$
Example 4.3.5 Using the Additive Interval Property
|
$$=\int_{-1}^{0} -x\:dx+ \int_{0}^{1}x \: dx$$ |
Theorem 4.3.4 |
|
$$=\frac{1}{2} +\frac{1}{2}$$ |
Triangle area | |
| \(=1\) |
|
|
If f and g are continuous on the closed interval \([a,b]\) and \(0 \leq f(x) \leq g(x)\) for \(a \leq x \leq b\), then the following properties hold true. First, the region's area bounded by the graph for \(f\) and the \(x\)-axis, between \(a\) and \(b\), must be nonnegative. Second, this area must be less than or equal to the area for the region bounded by the graph for \(g\) and the \(x\)-axis, between \(a\) and \(b|), as shown in Figure 4.3.10. These two properties are described in Theorem 4.3.5. Theorem 4.3.5 Preserving Inequality1. If \(f\) is integrable and nonnegative on the closed interval \([a,b]\), then
2. If \(f\) and \(g\) are integrable on the closed interval \([a,b]\) and \(f(x) \leq g(x)\) for every \(x\) in \([a,b]\) then
|
Internal Links
Parent Article: Calculus I 04 Integration








