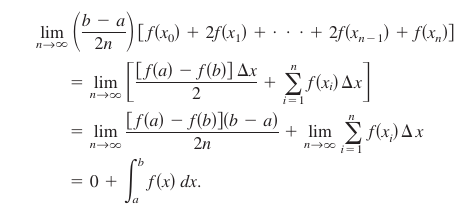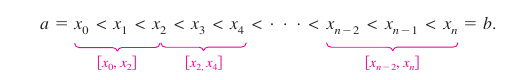Calculus I 04.06 Numerical Integration

Previous	Calculus I 04.05 Integration by Substitution
Next	Calculus I 05 Logarithmic, Exponential, and_Other Transcendental Functions

4.6 Numerical Integration[1]

• Approximate a definite integral using the Trapezoidal Rule.
• Approximate a definite integral using Simpson’s Rule.
• Analyze the approximate errors in the Trapezoidal Rule and Simpson’s Rule.

The Trapezoidal Rule[2]

The region's area can be approximated using four trapezoids. Figure 4.6.1

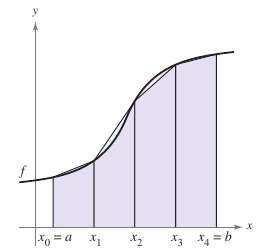
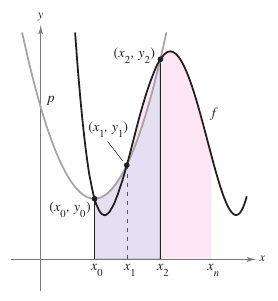
Some elementary functions simply do not have antiderivatives that are elementary functions. For example, the functions below lack any elementary function that is its antiderivative. $$\sqrt[3]{x} \sqrt{1-x},\:\:\sqrt{x} \cos x,\:\:\frac{\cos x}{x},\:\:\sqrt{1-x^3},\:\:\sin x^2$$ When evaluating a definite integral whose antiderivative cannot be found, or, cannot be easily applied even when the Fundamental Theorem of Calculus is still true, it is easier to resort to an approximation technique. Two techniques are The Trapezoidal Rule and The Simpson’s Rule, described here. One way to approximate a definite integral is to use \(n\) trapezoids, as shown in Figure 4.6.1. Let \(f\) be continuous and positive on the interval \([a,b]\). Therefore, the definite integral $$\int_{a}^{b} f(x)\:dx$$ represents the region's area bounded by the graph for \(f\) and the \(x\)-axis from \(x=a\) to \(x=b\). First, partition the interval \([a,b]\) into \(n\) subintervals, each \(\Delta x=(b-a)/n\), such that \(a = x_0 < x_1 < x_2 < \cdot \cdot \cdot < x_n=b\). 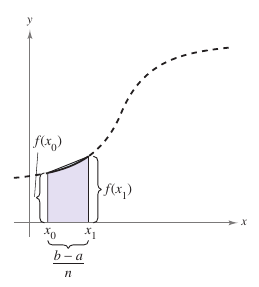Then form a trapezoid for each subinterval, as shown in Figure 4.6.2. The area for the \(i\)th trapezoid is

The area for one trapezoid. Figure 4.6.2

$$\text{Area for }i\text{th trapezoid}=\left [\frac{f(x_{i-1})+f(x_i)}{2} \right ] \left ( \frac{b-a}{n} \right ).$$ This implies the formula for summing the areas for \(n\) trapezoids is $$\text{Area }$$ $$=\left ( \frac{b-a}{n} \right ) \left [\frac{f(x_{0})+f(x_1)}{2} + \cdot \cdot \cdot +\frac{f(x_{n-1})+f(x_n)}{2} \right ] $$ $$=\left ( \frac{b-a}{2n} \right )[f(x_0)+f(x_1)+\cdot \cdot \cdot+f(x_{n-1})+f(x_n)]$$ $$=\left ( \frac{b-a}{2n} \right )[f(x_0)+2f(x_1)+\cdot \cdot \cdot+2f(x_{n-1})+f(x_n)].$$ Letting \(\Delta x= (b-a)/n\), produces the limit as \(n \to \infty\) which yields The result is summarized in Theorem 4.6.1.

Theorem 4.6.1 The Trapezoidal Rule

Let \(f\) be continuous on \([a,b]\). The Trapezoidal Rule for approximating \(\int_{a}^{b}f(x)dx\) is

$$\int_{a}^{b}f(x)\:dx \approx \left ( \frac{b-a}{2n} \right )[f(x_0)+2f(x_1)+\cdot \cdot \cdot+2f(x_{n-1})+f(x_n)].$$

As \(n \to \infty \), the right-hand side approaches \(\int_{a}^{b}f(x)dx\). Observe the coefficients in the Trapezoidal Rule have the following pattern.

1 2 2 2 ... 2 2 1

Example 4.6.1 Approximation with the Trapezoidal Rule

Trapezoidal approximations Figure 4.6.3

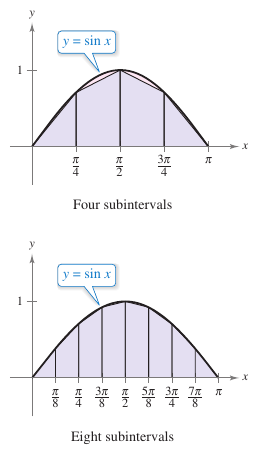
Use the Trapezoidal Rule to approximate $$\int_{0}^{\pi} \sin x \:dx$$ Compare the results for \(n=4\) and \(n=8\), as shown in Figure 4.6.3. Solution Let \(n=4\) and \(\Delta x = \pi/4\), yields $$\int_{0}^{\pi} \sin x \:dx$$ $$ \approx \frac{\pi}{8} \left ( \sin 0 + 2 \sin \frac{\pi}{4} + 2 \sin \frac{\pi}{2} + 2\sin \frac{3\pi}{4} + \sin \pi \right )$$ $$ = \frac{\pi}{8}(0+\sqrt{2}+2+\sqrt{2}+0)$$ $$=\frac{\pi(1+\sqrt{2}}{4}$$ \(\approx 1.896.\) Let \(n=8\) and \(\Delta x = \pi/8\), yields $$\int_{0}^{\pi} \sin x \:dx$$ $$ \approx \frac{\pi}{16} \left ( \sin 0 + 2 \sin \frac{\pi}{8} + 2 \sin \frac{\pi}{4} + 2\sin \frac{3\pi}{8} + 2\sin \frac{\pi}{2} \right .$$ $$ \left. +2 \sin \frac{5\pi}{8}+2 \sin \frac{3\pi}{4} + 2 \sin \frac{7\pi}{8}+ \sin \pi \right )$$ $$=\frac{\pi}{16} \left ( 2+2\sqrt{2}+4 \sin \frac{\pi}{8}+4 \sin\frac{3\pi}{8} \right )$$ \( \approx 1.974.\) This integral has an antiderivative found using techniques already discussed, the region's exact area is two. Thus illustrating that \(n \to \infty\) the approximation approaches the actual value.

Compare the Trapezoidal Rule with the Midpoint Rule discussed in Section 4.2. The Trapezoidal Rule takes the average function values at the endpoints on the subintervals. But the Midpoint Rule takes the function values on the subinterval midpoints.

$$\int_{a}^{b} f(x)\:dx \approx \sum_{i=1}^{n} f \left ( \frac{x_i+x_{i-1}}{2} \right ) \Delta x \:\:\:\:\:\:\:\:\:\:\:\:\:\: \color{red}{\text{Midpoint Rule}}$$

$$\int_{a}^{b} f(x)\:dx \approx \sum_{i=1}^{n} \left ( \frac{f(x_i)+f(x_{i-1})}{2} \right ) \Delta x \:\:\:\:\: \color{red}{\text{Trapezoidal Rule}}$$

Two important points concerning the Trapezoidal Rule and the Midpoint Rule. First, the approximation is more accurate as \(n\) increases. For instance, in Example 4.6.1, when \(n =16\), the Trapezoidal Rule yields an approximation at 1.994. Much more accurate than the 1.974 approximation when \(n=8.\) Second, although the Fundamental Theorem of Calculus can evaluate the integral in Example 4.6.1, this theorem cannot be used to evaluate an integral as simple as \(\int_{0}^{\pi} \sin x^2\:dx\) because \(\sin x^2\) has no elementary antiderivative. Yet, the Trapezoidal Rule can be applied to estimate this integral.

Simpson's Rule[3]

One way to view the trapezoidal approximation for a definite integral is to say that on each subinterval, a first-degree polynomial is used to approximate \(f\). Simpson’s Rule, named after the English mathematician Thomas Simpson (1710–1761)[4], takes this procedure one step further and approximates \(f\) by second-degree polynomials.

Before presenting Simpson's Rule, consider Theorem 4.6.2 for evaluating integrals for polynomials with degree two, or fewer.

Theorem 4.6.2 Integral for \(p(x)=Ax^2+Bx+C\)

If \(p(x)=Ax^2+Bx+C\), then

$$\int_{a}^{b} p(x)\:dx= \left ( \frac{b-a}{6} \right ) \left [ p(a)+4p \left ( \frac{a+b}{2} \right ) + p(b) \right ].$$

Proof

$$\int_{a}^{b} p(x)\:dx$$	$$=\int_{a}^{b} (Ax^2+Bx+C)\:dx$$
	$$=\left [ \frac{Ax^3}{3}+ \frac{Bx^2}{2}+Cx \right ]_{a}^{b}$$
	$$= \frac{A(b^3-a^3)}{3}+ \frac{B(b^2-a^2)}{2}+C(b-a)$$
	$$=\left ( \frac{b-a}{6} \right ) [2A(a^2+ab+b^2)+3B(b+a)+6C]$$

By expansion and collecting terms, the expression inside the brackets becomes $${\color{red}{\underbrace{\color{black}{(Aa^2+Ba+C)}}_{\color{red}{p(a)}}}}+{\color{red}{\underbrace{\color{black}{4\left [ A \left ( \frac{b+a}{2} \right )^2 + B\left ( \frac{b+a}{2} \right ) +C\right ]}}_{\color{red}{4p\frac{a+b}{2}}}}}+{\color{red}{\underbrace{\color{black}{(Ab^2+Bb+C)}}_{\color{red}{p(b)}}}}$$ and expressed as $$\int_{a}^{b} p(x)\:dx=\left ( \frac{b-a}{6} \right ) \left [ p(a)+4p \left ( \frac{a+b}{2} \right ) + p(b) \right ].$$

Figure 4.6.4

Applying Simpson’s Rule for approximating a definite integral by partitioning the interval \([a,b]\) into \(n\) subintervals, each \(\Delta x = (b-a)/2\) wide. The variable \(n\) must be even. The subintervals are grouped in pairs such that The double subintervals require that \(n\) be even. The approximation across each double subinterval \([x_{i-2},x_i]\) for \(f\) by a polynomial \(p\) with degree less than or equal to two. For example, on the subinterval \([x_0,x_2]\), choose the polynomial with the least degree passing through the points \((x_0,y_0),\:(x_1,y_1),\:\text{and}\:(x_2,y_2)\), as shown in Figure 4.6.4. By Theorem 4.6.2 and using \(p\) as an approximation for \(f\) on this subinterval produces $$\int_{x_0}^{x_2} f(x)\:dx$$ $$\approx\int_{x_0}^{x_2} p(x)\:dx$$ $$=\frac{x_2-x_0}{6} \left [ p(x_0)+4p \left ( \frac{x_0+x-2}{2} \right ) + p(x_2) \right ]$$ $$=\frac{ 2[(b-a)/n]}{6} [p(x_0)+4p(x_1)+p(x_2)]$$ $$=\frac{b-a}{3n}[f(x_0)+4f(x_1)+f(x_2)].$$ Repeating this procedure across the entire interval \([a,b]\) produces Theorem 4.6.3.

Theorem 4.6.3 Simpson's Rule

Let \(f\) be continuous on \([a,b]\) and let \(n\) be an even integer. Simpson's Rule for approximating \(\int_{a}^{b}f(x)\:dx\) is

$$\int_{a}^{b} f(x)\:dx \approx \frac{b-a}{3n} [f(x_i)$$	\(+4f(x_1)+2f(x_2)+4f(x_3)+\cdot \cdot \cdot\)
	\(+4f(x_{n-1})+f(x_n)].\)

As \(n \to \infty\), the right-hand side approaches \(\int_{a}^{b}f(x)\:dx\).
Observe the coefficients in Simpson's Rule have the following pattern

1 4 2 4 2 4...4 2 4 1

In Example 4.6.1, the Trapezoidal Rule was used to estimate \(\int_{0}^{\pi} \sin x\:dx\). In Example 4.6.2, Simpson's Rule is applied to the same integral.

Example 4.6.2 Approximation with Simpson’s Rule

use Simpson's Rule to approximate

$$\int_{0}^{\pi} \sin x\:dx.$$

Compare the results for \(n=4\) and \(n=8\).
Solution When \(n=4\), the result is

$$\int_{0}^{\pi} \sin x\:dx \approx \frac{\pi}{12} \left ( \sin 0 + 4 \sin \frac{\pi}{4}+ 2 \sin \frac{\pi}{2} + 4\sin \frac{3\pi}{4} + \sin \pi \right ) \approx 2.005.$$

When \(n=8\), the result is

$$\int_{0}^{\pi} \sin x\:dx \approx 2.0003.$$

Error Analysis

it is important to know how accurate an approximation technique is. Theorem 4.6.4 gives the formulas for estimating the error in Simpson’s Rule and the Trapezoidal Rule. In general the error \(E\) is the difference between \(\int_{a}^{b}f(x)\:dx\) and the approximation.

Theorem 4.6.4 Errors in the Trapezoidal Rule and Simpson’s Rule

If \(f\) has a continuous second derivative on \([a,b]\), then the error \(E\) in approximating \(\int_{a}^{b}f(x)\:dx\) by the Trapezoidal Rule is

$$ \left |E \right | \leq \frac{(b-a)^3}{12n^2} [\max | {f}''(x)|],\:\:\:\: a \leq x \leq b.$$

Trapezoidal Rule

if \(f\) has a continuous fourth derivative on \([a,b]\), then the error \(E\) is approximating \(\int_{a}^{b}f(x)\:dx\) by Simpson's Rule is

$$ \left |E \right | \leq \frac{(b-a)^5}{180n^4} [\max | f^{(4)}(x)|],\:\:\:\: a \leq x \leq b.$$

Simpson's Rule

Theorem 4.6.4 states that the errors generated by the Trapezoidal Rule and Simpson’s Rule have upper bounds dependent on the extreme values for \({f}''(x)\) and \(f^{(4)}(x)\) in the interval \([a,b]\). Furthermore, these errors can be made arbitrarily small by increasing \(n\), provided that \({f}''\) and \(f^{(4)}\) are continuous and therefore bounded in \([a,b]\).

Example 4.6.3 The Approximate Error in the Trapezoidal Rule

Figure 4.6.5

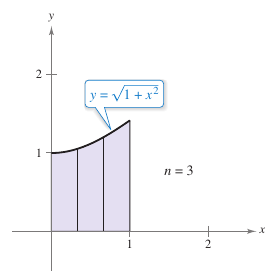
Determine a value for \(n\) such that the Trapezoidal Rule will approximate the value for $$\int_{0}^{1} \sqrt{1+x^2} \:dx$$ with an error that is less than or equal to 0.01. Solution Begin by letting \(f(x)=\sqrt{1+x^2}\) and finding the second derivative for \(f\). \({f}'(x)=x(1+x^2)^{-1/2}\) and \({f}''(x)(1+x^2)^{-3/2}\) The maximum value for \(| {f}''(x)|\) on the interval \([0,1]\) is \(|{f}''(0)|=1\). By Theorem 4.6.4 the result is $$ \left | E \right | \leq \frac{(b-a)^3}{12n^2} \left |{f}''(0) \right |=\frac{1}{12n^2}(1)=\frac{1}{12n^2}.$$ To obtain an error \(E\) that is less than 0.01 choose \(n\) such that $$\frac{1}{12n^2} \leq \frac{1}{100}.$$ $$100 \leq 12n^2 \rightarrow n \leq \sqrt{ \frac{100}{12}} \approx 2.89$$ Choose \(n=3\), because \(n\) must be greater or equal to 2.89, and apply the Trapezoidal Rule, as shown in Figure 4.6.5, to produce $$\int_{0}^{1} \sqrt{1+x^2} \:dx$$ $$ \approx \frac{1}{6} \left [ \sqrt{1+0^2} + 2 \sqrt{1+ \left ( \frac{1}{3}\right)^2} + 2 \sqrt{1+ \left ( \frac{2}{3}\right)^2} + \sqrt{1+1^2} \right ]$$ \( \approx 1.154.\) By adding and subtracting the error from the estimate yields $$1.144 \leq \int_{0}^{1} \sqrt{1+x^2} \:dx \leq 1.164$$

Internal Links

Parent Article: Calculus I 04 Integration