Calculus II 07.03 Volume The Shell Method

Previous	Calculus II 07.02 Volume The Disk Method
Next	Calculus II 07.04 Arc Length and Surfaces for Revolution

7.3 Volume The Shell Method

• Find the volume for a rotated solid using the shell method.
• Compare The Disk Method and The Shell Method.

The Shell Method

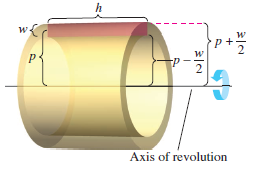Figure 7.3.1 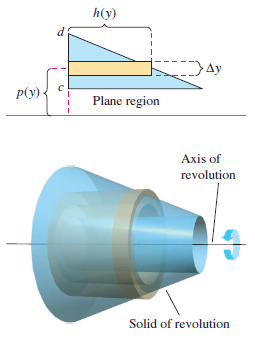Figure 7.3.2

The Shell Method gets its name because it uses cylindrical shells to find the solid's volume. Consider a representative rectangle as shown in Figure 7.3.1, where \(w\) is the rectangle's width, \(h\) is the rectangle's height, and \(p\) is the distance between the rotation axis and the rectangle's \(center\). When this rectangle is rotated about the axis, it forms a cylindrical shell (or tube) with thickness \(w\). To find the volume of this shell, consider two cylinders, one inside the other. The radius for the larger cylinder corresponds to the shell's outer radius. The radius for the smaller cylinder corresponds to the shell's inner radius. Because \(p\) is the average radius for the shell, the formula for the outer radius is $$ p+\frac{w}{2} \:\:\:\: \color{red}{ \text{Outer radius}}$$ and the formula for the inner radius is $$ p-\frac{w}{2} \:\:\:\: \color{red}{ \text{Inner radius}}$$ This produces the volume for the entire shell Shell Volume $$=\pi(p+\frac{w}{2})^{2}h-\pi(p-\frac{w}{2})^{2} $$ \(=2\pi phw\) \(=2\pi(average \: radius)(height)(thickness)\) The plane region in Figure 7.3.2 is rotated about a line to form a solid. Consider a horizontal rectangle with width \(\Delta y\). As the plane region is revolved about a line parallel to the axis, the rectangle generates a representative shell whose volume is $$\Delta V = 2 \pi \left[ p(y)h(y) \right ]\: \Delta y $$ You can approximate the solid's volume by \(n\) such shells with thickness \(\Delta y\), height \(h(y_{i})\), and average radius \(p(y_{i})\). $$Solid \: Volume \approx \sum_{i=1}^{n} 2 \pi \left[ p(y_{i})h(y_{i}) \right ] \Delta y = 2 \pi \sum_{i=1}^{n} \left [ p(y_{i})h(y_{i}) \right ] \Delta y $$ This approximation improves as \(\left \| \Delta \right \| \rightarrow 0(n\rightarrow \infty )\). Solid Volume $$= \lim_{ \left \| \Delta \right \| \rightarrow 0} 2 \pi \left [ p(y)h(y) \right ]\: \Delta y$$ $$ = 2 \pi \int_{c}^{d} \left [ p(y)h(y) \right ]\: \Delta y $$

Definition 7.3.1 The Shell Method

To find the volume for a rotated solid with the shell method,
use a formulas below. (See Figure 7.3.3)

Horizontal Axis Rotation		Vertical Axis Rotation
Volume	$$(= V = 2 \pi \int_{e}^{d}p(y)h(y)\:dy \:\:\:\: $$	Volume	$$= V = 2 \pi \int_{a}^{b}p(x)h(d)\:dx $$

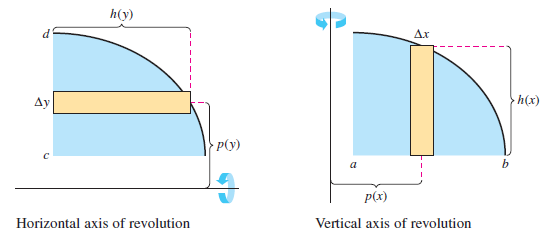
Figure 7.3.3

Example 7.3.1 Using The Shell Method to Find Volume

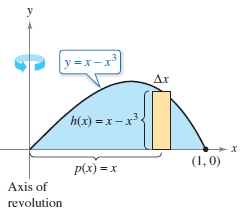Figure 7.3.4

Find the volume for the rotated solid formed by revolving the region bounded by $$y=x-x^{3} $$ and the \(x\)-axis \((0 \leq x \leq 1)\) about the \(y\)-axis. Solution Because the axis is vertical, use the vertical representative rectangle, as shown in Figure 7.3.4. The width \(\Delta x\) indicates that \(x\) is the integration variable. The distance from the rectangle's center to the axis is \(p(x)=x\), and the rectangle's height is \(h(x)= x-x^{3}\). Because \(x\) ranges from 0 to 1, apply the shell method to find the solid's volume. \(V\) $$ = 2 \pi \int_{a}^{b}p(x)h(x)\:dx $$ Vertical Axis Formula $$ = 2 \pi \int_{0}^{1}x \left(x-x^{3} \right)\:dx $$ Substitute the shell formulas $$ = 2 \pi \int_{0}^{1}\left(-x^{4}+x^{2} \right)\:dx \:\:\:\: $$ Simplify $$ = 2 \pi \left[ -\frac{x^{5}}{5}+\frac{x^{3}}{3} \right]_{0}^{1} $$ Integrate $$ = 2 \pi \left( -\frac{1}{5}+\frac{1}{3} \right) = \frac{4\pi}{15} $$

Example 7.3.2 Using the Shell Method to Find Volume

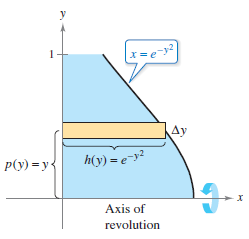Figure 7.3.5

Find the volume for the rotated solid formed by revolving the region bounded by the graph for $$x=e^{-y^{2}} $$ and the \(y\)-axis \((0 \leq y \leq 1)\) about the \(x\)-axis. Solution Because the axis is horizontal, use a horizontal representative rectangle, as shown in Figure 7.3.5. The width \(\Delta y\) indicates that \(y\) is the integration variable. The distance from the rectangle's center of the rectangle to the axis is \(p(y)=y\), and the rectangle's height is \(h(y)=e^{-y^{2}}\). Because \(y\) ranges from 0 to 1, the solid's volume is \(V\) $$ = 2 \pi \int_{c}^{d}p(y)h(y)\:dy $$ Horizontal Axis Formula $$ = 2 \pi \int_{0}^{1}ye^{-y^{2}}\:dy $$ Substitute the shell formulas $$ = 2 \pi \left [ e^{-y^{2}} \right ]_{0}^{1} $$ Integrate $$ = \pi \left( 1-\frac{1}{e} \right) \approx 1.986 $$

Comparing the Disk and Shell Methods

The disk and shell methods can be distinguished as follows. For the disk method, the representative rectangle is always perpendicular to the rotation axis, whereas for the shell method, the representative rectangle is always parallel to the rotation axis, as shown in Figure 7.32.

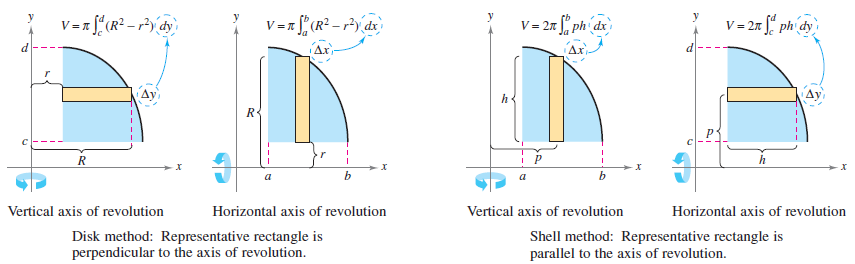
Figure 7.3.6

Example 7.3.3 Shell Method Preferable

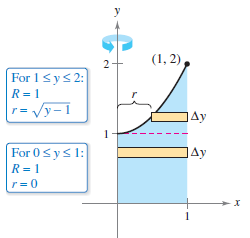Disk Method Figure 7.3.7 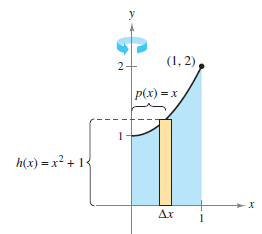Shell Method Figure 7.3.8

Sometimes one method is more convenient than the other. Example 7.3.3 illustrates a case in which the shell method is preferable. Find the volume for the solid formed by revolving the region bounded by the graphs $$y=x^{2}+1, \: y=0, \: x=0 \text{, and } x=1 $$ about the \(y\)-axis. Solution In Section 7.2, Example 7.2.4 demonstrated that The Washer Method requires two integrals to determine the volume for this solid. See Figure 7.3.7. $$V$$ $$=\pi \int_{0}^{1}(1^{2}-0^{2})\:dy+\pi \int_{1}^{2} \left[ 1^{2}-(\sqrt{y-1})^{2} \right]\:dy \:\:\:\: $$ Apply The Washer Method $$=\pi \int_{0}^{1} 1\:dy+\pi \int_{1}^{2} \left( 2-y \right) \:dy $$ Simplify $$=\large \pi \left[ y \right]_{0}^{1} \large + \pi \left[ 2y-\frac{y^{2}}{2} \right]_{1}^{2} $$ Integrate $$= \pi + \pi \left(4-2-2+ \frac{1}{2} \right) = \frac{3 \pi}{2}$$ Figure 7.3.8 demonstrates that the shell method requires only one integral to find the volume. $$V$$ $$ = 2 \pi \int_{a}^{b}p(x)h(x)\:dx $$ Apply The Shell Method $$ = 2 \pi \int_{0}^{1}x(x^{2}+1)\:dx \:\:\:\: $$ Substitute the integral formulas $$ = 2 \pi \left[ -\frac{x^{4}}{4}+\frac{x^{3}}{3} \right]_{0}^{1} $$ Integrate $$ = 2 \pi \left( \frac{3}{4} \right) = \frac{3\pi}{2}$$ Consider the solid formed by revolving the region in Example 7.3.3 about the vertical line \(x=1\). Would the resulting solid have a greater volume or a smaller volume than the solid in Example 7.3.3? Without integrating, you should be able to reason that the resulting solid would have a smaller volume because "more" region would be closer to the axis. To confirm this, try solving the integral $$V = 2 \pi \int_{0}^{1} (1-x)(x^{2}+1)\:dx\:\:\:\: \color{red}{p(x)=1-x} $$ which gives the solid's volume.

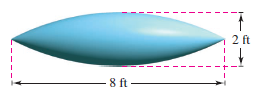
Example 7.3.4 Volume for a Pontoon

Pontoon Figure 7.3.9 Disk Method Figure 7.3.10

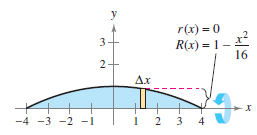
A pontoon has the shape shown in Figure 7.3.4. This pontoon is designed by rotating the graph for $$y=1-\frac{x^{2}}{16}, \: -4 \leqslant x \leqslant 4 $$ about the \(x\)-axis, where \(x\) and \(y\) are measured in feet. Find the pontoon's volume. Solution Refer to Figure 7.3.10 and use the disk method as shown. $$V$$ $$ = \pi \int_{-4}^{4} \left( 1-\frac{x^{2}}{16} \right)^\:dx $$ Apply the disk method $$ = \pi \int_{-4}^{4} \left( 1-\frac{x^{2}}{8}+\frac{x^{4}}{256} \right)\:dx $$ Simplify $$ = \pi \left[ x-\frac{x^{3}}{24}+\frac{x^{5}}{1280} \right]_{-4}^{4} $$ Integrate $$ = \frac{64 \pi}{15} \approx 13.4 \text{ cubic feet }$$ To use the shell method in Example 7.3.4, solve for \(x\) in \(y\) terms, in the equation $$y=1-\frac{x^{2}}{16} $$ and then evaluate an integral that requires a \(u\)-substitution. Solving for \(x\) is very difficult, or even impossible, in some cases. In such cases, use a vertical rectangle (with width \( \Delta x\)), thus making \(x\) the integration variable. The axis orientation position (horizontal or vertical) then determines the method needed. This is shown in Example 7.3.5.

Example 7.3.5 Shell Method Necessary

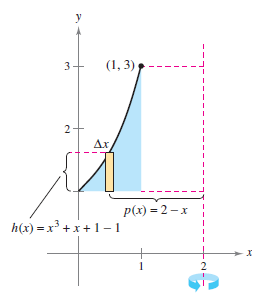Figure 7.3.11

Find the volume for the solid formed by revolving the region bounded by the graphs for \(y=x^{3}+x+1, \: y=1, \: \text{and} \: x=1\) about the line \(x=2\), as shown in Figure 7.36 Solution In the equation \(y=x^{3}+x+1\), \(x\) is not easily solved in terms \(y\). (See Section 3.8 for a discussion at the end) Therefore, the integration variable must be \(x\), and a vertical representative rectangle chosen. Because the rectangle is parallel to the rotation axis, use the shell method. $$V$$ $$ = 2 \pi \int_{a}^{b}p(x)h(x)\:dx $$ Apply the shell method $$ = 2 \pi \int_{0}^{1} (2-x)(x^{3} + x + 1 - 1)\:dx \:\:\:\:$$ Substitute the equations $$ = 2 \pi \int_{0}^{1} (-x^{4} + 2x^{3}-x^{2}+2x ) \: dx $$ Simplify $$ = 2 \pi \left[ -\frac{x^{5}}{5} + \frac{x^{4}}{2} - \frac{x^{3}}{3}+x^{2} \right]_{0}^{4} $$ Integrate $$ = 2 \pi \left( -\frac{1}{5}+\frac{1}{2}-\frac{1}{3}+1 \right) =\frac{29 \pi}{15}$$

Internal Links

Parent Article: Calculus II 07 Integration Applications