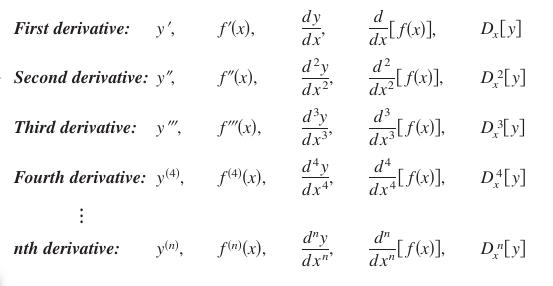Calculus I 02.03 Product Rule, Quotient Rule, and Higher-Order Derivatives
| Previous | Calculus I 02.02 Basic Differentiation Rules and Change Rate |
| Next | Calculus I 02.04 The Chain Rule |
Contents
Product Rule, Quotient Rule and Higher-Order Derivatives
- Product Rule derivatives.
- Quotient Rule derivatives.
- Trigonometric derivatives.
- Higher-Order derivatives.
The Product Rule
Section 2.2 described how the derivative for two summed functions was equal to summing their separate derivatives. The Product and Quotient Rules for two functions are more complex
Theroem 2.3.1 The Product Rule
The product with two differentiable functions \(f\) and \(g\) is itself differentiable. The derivative for \(fg\) is the first function times the derivative for the second plus the second function times the derivative for the first. The expression is
- $$\frac{d}{dx}[f(x)g(x)]=f(x){g}'(x)+g(x){f}'(x).$$
Another form is
- $$\frac{d}{dx}[f(x)g(x)]={f}'(x)g(x)+f(x){g}'(x).$$
Which is easier to use with products that include three or more factors.
Proof The Sum Rule was a straight forward proof. Complex proofs involve require clever steps. This proof uses such a step -- subtracting and adding the same quantity -- which is shown in red.
|
$$\frac{d}{dx}[f(x)g(x)]$$ |
$$=\lim_{\Delta x \to 0} \frac{f(x+\Delta x)+g(x+\Delta x)-f(x)g(x)}{\Delta x}$$ |
|
$$=\lim_{\Delta x \to 0} \frac{f(x+\Delta x)+g(x+\Delta x){\color{red}{-f(x+\Delta x)(gx)+f(x+\Delta x)(gx)}}-f(x)g(x)}{\Delta x}$$ | |
|
$$=\lim_{\Delta x \to 0} \left [ f(x+\Delta x)\frac{g(x+\Delta x)-g(x)}{\Delta x}+g(x)\frac{f(x+\Delta x)-f(x)}{\Delta x} \right ]$$ | |
|
$$\lim_{\Delta x \to 0} \left [ f(x+\Delta x)\frac{g(x+\Delta x)-g(x)}{\Delta x}\right ]+ \lim_{\Delta x \to 0} \left [g(x)\frac{f(x+\Delta x)-f(x)}{\Delta x} \right ]$$ | |
|
$$\lim_{\Delta x \to 0} f(x+\Delta x)\cdot \lim_{\Delta x \to 0}\frac{g(x+\Delta x)-g(x)}{\Delta x}+ \lim_{\Delta x \to 0} g(x)\cdot \lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x} $$ | |
| \(=f(x){g}'+g(x){f}'(x)\) |
Note that \(\lim_{\Delta x \to 0} f(x+\Delta x)=f(x)\) because \(f\) is differentiable and is therefore continuous.
The Product Rule can be extended to cover products with more than two factors. For example, if \(f\), \(g\), and \(h\) are differentiable functions with \(x\), then
- $$\frac{d}{dx}[f(x)g(x)h(x)]={f}'(x)g(x)h(x)+f(x){g}'(x)+f(x)g(x){h}'(x).$$
For example, the derivative for \(y=x^2 \sin x \cos x\) is
| |
|
\(=2x \sin x \cos x+ x^2 \cos x \cos x+ x^2 \sin x (-\sin x)\) | |
| \(=2x \sin x \cos x + x^2(\cos^2x - \sin^2 x)\). |
The derivative for a product with two functions is not, in general, given by the product for the derivatives for the two functions. For example, compare the product and derivatives for
- \(f(x)=3x-2x^2\)
and
- \(g(x)=5+4x\)
with the derivative in Example 2.3.1 below.
Example 2.3.1 Using the Product Rule
Find the derivative for \(h(x)=(3x-2x^2)(5+4x)\).
Solution
In Example 2.3.1 the derivative can be found with or without the Product Rule. To find it without the Product Rule write the expression as
| \(D_x[(3x-2x^2)(5+4x)]\) | \(=D_x[-8x^3+2x^2+15x]\) |
| \(=-24x^2+4x+15.\) |
Example 2.3.2 Using the Product Rule
Find the derivative for \(y=3x^2 \sin x\).
Solution
|
$$=3x^2\frac{d}{dx}[\sin t] + \sin x \frac{d}{dx}[3x^2]$$ |
| \(=3x^2 \cos x + (\sin x)(6x)\) | |
| \(=3x^2\cos x + 6x \sin x\) | |
| \(=3x(x \cos x+ 2 \sin x)\) |
Example 2.3.3 Using the Product Rule
Find the derivative for \(y=3x \cos x -2 \sin x\).
Solution
|
$$\color{red}{\overbrace{\color{black}{(2x) \left ( \frac{d}{dx}[\cos x]\right ) + (\cos x)\left ( \frac{d}{dx}[2x]\right ) }}^{\color{red}{\text{Product Rule}}}}\color{red}{\overbrace{\color{black}{ -2\frac{d}{dx}[\sin x] }}^{\color{red}{\text{Constant Multiple Rule}}}} $$ |
| \(=(2x)(-\sin x) + (\cos x)(2)-2(\cos x)\) | |
| \(=-2x \sin x\) |
The Quotient Rule
Theorem 2.3.2 The Quotient Rule
The quotient \(f/g\) with two differentiable functions \(f\) and \(g\) is itself differentiable at all values for \(x\) where \(g(x) \neq 0\). The derivative for \(f/g\) is given by the denominator times the derivative for the numerator minus the numerator times the derivative for the denominator, all divided denominator squared.
- $$\frac{d}{dx} \left [ \frac{f(x)}{g(x)} \right ]=\frac{g(x){f}'(x)-f(x){g}'(x)}{[g(x)]^2},\:\:\:\:g(x) \neq 0$$
Proof The key to proving The Quotient Rule is subtracting and adding the same quantity, as noted in red below.
Note that \(\lim_{\Delta x \to 0} g(x+\Delta x)=g(x)\) because \(g\) is differentiable and therefore is continuous.
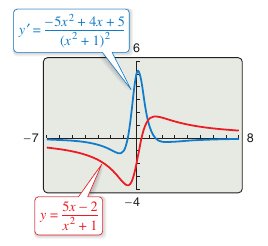
Example 2.3.4 Using the Quotient Rule
 Graph comparing a function and its derivative. Figure 2.3.1 |
Find the derivative for
Solution
Note the parentheses in Example 2.3.4. Applying parentheses is recommended for all types of differentiation problems. For example, with the Quotient Rule, enclose all factors and derivatives in parentheses, and to pay special attention to the subtraction required in the numerator. When differentiation rules were introduced the need for rewriting before differentiating was emphasized. The next example illustrates this point with the Quotient Rule. |
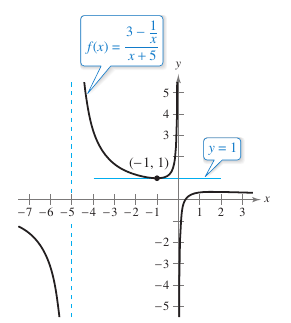
Example 2.3.5 Rewriting Before Differentiating
 The line \(y=1\) is tangent to the graph for \(f(x)\) at the point \((-1,1)\). Figure 2.3.2 |
Find the derivative for
Solution  Then, using the point-slope for a line equation produces \(y=1\) at \((-1,1)\), as shown in Figure 2.3.2. |
Not every quotient function needs the Quotient Rule to find the derivative. For example, each quotient in Example 2.3.6 can be considered as a product with constants times a function for \(x\). In such cases, it is more convenient to use the Constant Multiple Rule.
Example 2.3.6 Using the Constant Multiple Rule
| Original Function | Rewrite | Differentiate | Simplify | |
|---|---|---|---|---|
| a. |
$$y=\frac{x^2+3x}{6}$$ |
$$y=\frac{1}{6}(x^2+3x)$$ |
$${y}'=\frac{1}{6}(2x+3)$$ |
$${y}'=\frac{2x+3}{6}$$ |
| b. |
$$y=\frac{5x^4}{8}$$ |
$$y=\frac{5}{8}x^4$$ |
$${y}'=\frac{5}{8}(4x^3)$$ |
$${y}'=\frac{5}{2}x^3$$ |
| c. |
$$y=\frac{-3(3x-2x^2)}{7x}$$ |
$$y=-\frac{3}{7}(3-2x)$$ |
$${y}'=-\frac{3}{7}(-2)$$ |
$${y}'=\frac{6}{7}$$ |
| d. |
$$y=\frac{9}{5x^2}$$ |
$$y=\frac{9}{5}(x^{-2})$$ |
$${y}'=\frac{9}{5}(-2x^{-3})$$ |
$${y}'=-\frac{18}{5x^3}$$ |
In Section 2.2, the Power Rule was proved only for the case where the exponent \(n\) is a positive integer greater than 1. The next Example 2.3.7 extends the proof to include negative integer exponents.
Example 2.3.7 Power Rule: Negative Integer Exponents
If \(n\) is a negative integer, then there exists a positive integer \(k\) such that \(n=-k\). Therefore, by the Quotient Rule, the expression can be written as.
|
$$=\frac{d}{dx} \left [ \frac{d}{dx} \frac{1}{x^k} \right]$$ | |
|
$$= \frac{x^k(0)-(1)(kx^{k-1})}{(x^k)^2}$$ |
Quotient and Power Rules | |
|
$$=\frac{0-kx^{k-1}}{x^{2k}}$$ | ||
| \(=-kx^{-k-1}\) | ||
| \(=nx^{n-1}.\) | \(n=-k\) | |
|
$$=nx^{n-1}$$ |
Power Rule |
Which proves the Power Rule is valid for any integer.
Trigonometric Function Derivatives
Using the derivatives for sine and cosine function, finding the derivatives for the four remaining trigonometric functions using the Quotient Rule.
Theorem 2.3.3 Trigonometric Function Derivatives
|
$$\frac{d}{dx} [\tan x]=\sec^2 x$$ |
$$\frac{d}{dx}[\cot x]= -\csc^2 x$$ |
|
$$\frac{d}{dx} [\sec x]=\sec x \tan x$$ |
$$\frac{d}{dx} [\csc x]=\csc x \cot x$$ |
Proof Consider \(\tan x =(\sin x)/(\cos x)\) and the identities \(\sin^2 x+ \cos^2 x =1 \) and \(\sec x \ 1/(\cos x)\). Applying the Quotient Rule produces
|
$$=\frac{d}{dx} \left [ \frac{\sin x}{\cos x} \right ]$$ | |
|
$$=\frac{(\cos x)(\cos x)-(\sin x)(-\sin x)}{\cos^2 x}$$ |
Apply Quotient Rule. | |
|
$$=\frac{\cos^2 x + \sin^2 x}{\cos^2 x}$$ | ||
|
$$=\frac{1}{\cos^2 x}$$ | ||
| \(=\sec^2 x.\) |
Proving the three remaining parts is similar and left as an exercise.
Example 2.3.8 Differentiating Trigonometric Functions
| Function | Derivative | ||
|---|---|---|---|
| a. | \(y=x-\tan x\) |
$$\frac{d}{dx}$$ |
$$=1- \sec^2 x$$ |
| b. | \(y=x \sec x\) | \({y}'\) | \(=x(\sec x \tan x)+(\sec x)(1)\) |
| \(=(\sec x)(1+ x \tan x )\) | |||
Example 2.3.9 The Derivatives in Different Forms
Differentiate both forms for
- $$y=\frac{1-\cos x}{\sin x} = \csc x - \cot x.$$
Solution
| First form: |
$$y$$ |
$$=\frac{1- \cos x}{\sin x}$$ | ||
|
$${y}'$$ |
$$=\frac{(\sin x)(\sin x)- (1- \cos x)(\cos x)}{\sin^2 x}$$ | |||
|
$$=\frac{\sin^2 x-\cos x +\cos^2 x}{\sin^2 x}$$ | ||||
| ||||
| Second form: |
\(y\) |
\(=\csc x - \cot x\) | ||
| \({y}'\) | \(=\csc x \cot x + \csc^2 x\) |
To show both derivatives are equal, rewrite the expression as
|
$$=\frac{1}{\sin^2 x}-\frac{\cos x}{\sin^2 x}$$ |
|
$$=\frac{1}{\sin^2 x}- \left (\frac{1}{\sin2 x} \right ) \left ( \frac{\cos x}{\sin x} \right )$$ | |
| \(=\csc^2 x-\csc x \cot x.\) |
Table 2.3.1 below shows derivatives after simplification. Note that a simplified form lacks negative exponents and combines like terms.
| Table 2.3.1 | ||
|---|---|---|
| \({f}'(x)\) After Differentiating | \({f}'(x)\) After Simplifying | |
| Example 1 |
\((3x-2x^2)(4)+(5+4x)(3-4x)\) |
\(-24x^2+4x+15\) |
| Example 2 | \((2x)(-\sin x)+(\cos x)(2)-2(\cos x)\) |
\(-2x \sin x\) |
| Example 3 |
$$\frac{(x^2+1)(5)-(5X-2)(2x)}{(x^2+1)^2}$$ |
$$\frac{-5x^2+4x+5}{(x^2+1)^2}$$ |
| Example 4 |
$$\frac{(x^2+5x)(3)-(3x-1)(2x+5)}{(x^2+5x)^2}$$ |
$$\frac{-3x2+2x+5}{(x^2+5x)^2}$$ |
| Example 5 |
$$\frac{(\sin x)(\sin x)-(1-\cos x)(\cos x)}{\sin^2 x}$$ |
$$\frac{1-\cos x}{\sin^2 x}$$ |
Higher-Order Derivatives
Just as differentiating a position function produces a velocity function, differentiating the velocity function produces the acceleration. This means differentiating the position function twice, or, by taking a second derivative.
| \(s(t)\) | Position function |
| \(v(t)={s}'(t)\) | Velocity function |
| \( a(t)={v}'(t)={s}''(t) \) | Acceleration function |
The second derivative is a higher-order derivative. You can define derivatives of any positive integer order. For instance, the third derivative is the derivative for the second derivative. Higher-order derivatives are denoted as shown below.
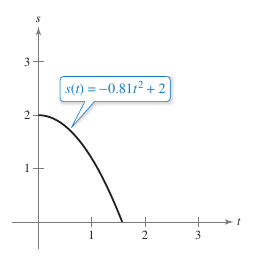
Example 2.3.10 Finding the Acceleration Due to Gravity
 Acceleration Due to Gravity on the Moon. Figure 2.3.3 |
Because the Moon has no atmosphere, a falling object on the moon encounters no air resistance. In 1971, astronaut David Scott demonstrated that a feather and a hammer fall at the same rate on the moon. The position function for any falling object on the Moon is
where \(s(t)\) is the height in meters and \(t\) is the time in seconds, as shown in Figure 2.3.3. What is the ratio between Earth's gravity and the Moon's?
The acceleration due to the Moon's gravity is \(-1.62\) meters per second squared. The acceleration due to the Earth's gravity is \(-9.8\) meters per second squared. This makes the ratio between them
|
Internal Links
Parent Article: Calculus I 02 Differentiation
