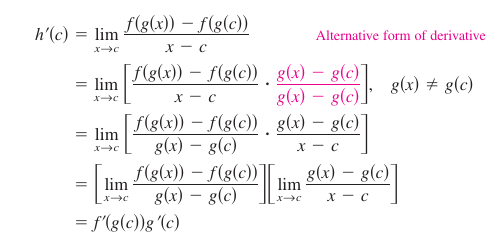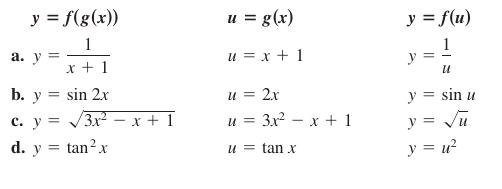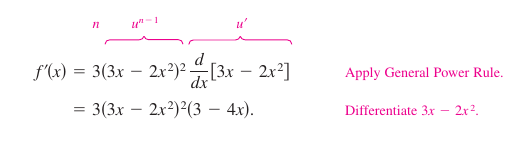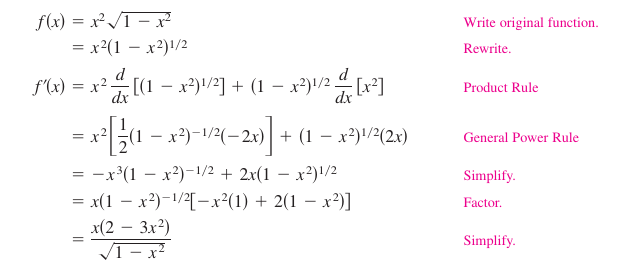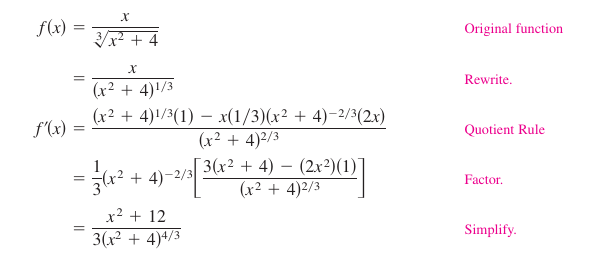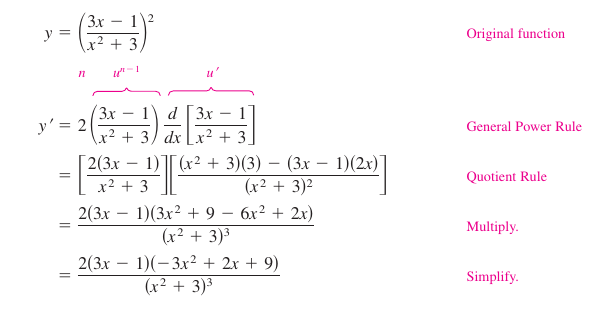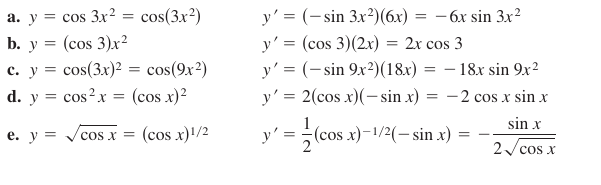Calculus I 02.04 The Chain Rule

Previous	Calculus_I_02.03_Product_Rule,_Quotient_Rule,_and_Higher-Order_Derivatives
Next	Calculus_I_02.05_Implicit_Differentiation

The Chain Rule

• Use the Chain Rule to find the derivative for a composite function.
• Use the General Power Rule to find a derivative.
• Use algebra to simplify a derivative.
• Use the Chain Rule to find the derivative for a trigonometric function.

The Chain Rule finds derivatives for composite functions and adds a surprising versatility to the rules discussed previously. For example, compare the functions shown below. Those on the left can be differentiated without the Chain Rule. Those on the right are differentiated with more ease by using the Chain Rule.

Without the Chain Rule	With the Chain Rule
\(y=x^2+1\)	\(y=\sqrt{x^2+1}\)
\(y=\sin x\)	\(y=\sin 6x\)
\(y=3x+2\)	\(y=(3x+2)^5\(
\(y=x + \tan x\)	\(y=x+ \tan x^2\)

The Chain Rule stats that if \(y\) changes \(dy/du\) times as fast as \(u\), and \(u\) changes \(du/dx\) times as fast as \(x\), then \(y\) changes \((dy/du)(du/dx)\) times as fast as \(x\).

Example 2.4.1 The Derivative for a Composite Function

Axle 1: \(y\) revolutions per minute Axle 2: \(u\) revolutions per minute Axle 3: \(x\) revolutions per minute Figure 2.4.1

A gear set, as shown in Figure 2.24, is built such that the second and third gears are on the same axle. As the first axle revolves, it drives the second axle, which in turn drives the third axle. Let \(y\), \(u\), and \(x\) represent the revolutions per minute for the first, second, and third axles, respectively. Find \(dy/du\), \(du/dx\), and \(dy/dx\). Show that $$\frac{dy}{dx}= \frac{dy}{du} \cdot \frac{du}{dx}.$$ Solution Because the second gear's circumference is three times the first, the first axle must make three revolutions to turn the second axle once. The second axle must make two revolutions to turn the third axle once. This can be expressed as $$\frac{dy}{du}=3 \text{ and } \frac{du}{dx} =2.$$ Combine these results to find the first axle must make six revolutions to turn the third axle once. This can be expressed as The change rate for \(y\) with respect to \(x\) is the product between the change for \(y\) with respect to \(u\) and the change rat for \(u\) with respect to \(x\).

Theorem 2.4.1 The Chain Rule

If \(y=f(u)\) is a differentiable function for \(u\) and \(u=g(x)\) is a differentiable function for \(x\), then \(y=f(g(x))\) is a differentiable function for \(x\) and

$$\frac{dy}{dx}=\frac{dy}{du}\cdot\frac{du}{dx}$$

or, equivalently,

$$\frac{d}{dx}[f(g(x))]= {f}'(g(x)){g}'(x).$$

Proof Let \(h(x)=f(g(x))\). Then, using the alternative form show that \(x=c\).

\({h}'(c)={f}'(g(c)){g}'(c).\)

An important consideration is \(g\)'s behavior as \(x\) approaches \(c\). A problem occurs when there are values for \(x\), other than \(c\), such that

\(g(x)=g(c).\)

For simplicity assume that \(g(x) \neq g(c)\) for \(x\) values other than \(c\). In proofs for the Product Rule and the Quotient Rule, the same quantity was added and subtracted to obtain the desired form. A similar technique is used here, multiplying and dividing by the same, nonzero, quantity. Note that because \(g\) is differentiable, it is also continuous, and it follows that \(g(x)\) approaches \(g(c)\) as \(x\) approaches \(c\).

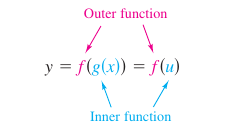
When applying the Chain Rule think about the composite function \(f \circ g\) as having two parts, and inner and outer part.

The derivative for \(y=f(u)\) is the derivative for the outer function, at the inner function \(u\) times the derivative for the inner function.

\({y}'={f}'(u) \cdot {u}'\)

Example 2.4.2 Decomposing a Composite Function

Example 2.4.3 Using the Chain Rule

Find \(dy/dx\) for

\(y=(x^2+1)^3.\)

Solution Let the inside function be \(u=x^2+1\) and the outer function be \(y=u^3\). Apply the Chain Rule and

$$\frac{dy}{dx}=\color{red}{\underbrace{\color{black}{3(x^2+1)^2}}_{\color{red}{\frac{dy}{du}}}}\color{red}{\underbrace{\color{black}{(2x)}}_{\color{red}{\frac{du}{dx}}}}=6x(x^2+1)^2.$$

The General Power Rule

Example 2.4.3 used a common composite function, \(y=[u(x)]^n\). The rule for differentiating such functions is called General Power Rule. It is a special case for the Chain Rule.

Theorem 2.4.2 The General Power Rule

If \(y=[u(x)]^n\), where \(u\) is a differentiable function for \(x\) and \(n\) is a rational number, then

$$\frac{dy}{dx}=n[u(x)]^{n-1}\frac{du}{dx}$$

or, equivalently,

$$\frac{d}{dx}[u^n]=nu^{n-1}{u}'$$.

Proof Because \(y=[u(x)]^n=u^n\), apply the Chain Rule to obtain

$$\frac{dy}{dx}$$	$$=\left ( \frac{dy}{du} \right ) \left ( \frac{du}{dx} \right )$$
	$$=\frac{d}{du}[u^n]\frac{du}{dx}.$$

Applying The Simple Power Rule produces \(D_u[u^n]=nu^{n-1}\), and it follows that

$$\frac{dy}{dx}=nu^{n-1}\frac{du}{dx}.$$

Example 2.4.4 Applying the General Power Rule

Find the derivative for \(f(x)=(3x-2x^2)^3.\)
Solution Let \(u=3x-2x^2\). Then

\(f(x)=(3x-2x^2)^3= u^3.\)

Apply the General Power Rule produces the derivative

Example 2.4.5 Differentiating Functions Involving Radicals

The derivative for \(f\) is 0 at \(x=0\) and is undefined at \(x= \pm 1\). Figure 2.4.2

Find all points on the graph for \(f(x)=\sqrt[3]{(x^2-1)^2}\) for which \({f}'(x)=0\) and those for which \({f}'(x)\) does not exist. Solution Begin by rewriting the function as \(f(x)=(x^2-1)^{2/3}.\) Apply the General Power Rule with \(u=x^2-1\) produces $${f}'(x)$$ $$=\color{red}{\overbrace{\color{black}{\frac{2}{3}}}^{\color{red}{\text{n}}}}\color{red}{\overbrace{\color{black}{(x^2-1)^{-1/3}}}^{\color{red}{\text{u^{n-1}}}}}\color{red}{\overbrace{\color{black}{(2x)}}^{\color{red}{\text{{u}'}}}} $$     Apply General Power Rule. $$=\frac{4x}{3\sqrt[3]{x^2-1}}.$$     Write in radical form. Therefore, \({f}'(x)=0\) when \(x=0\), and \({f}'(x)\) does not exist when \(x = \pm 1\), as shown in Figure 2.4.2.

Example 2.4.6 Differentiating Quotients with Constant Numerators

Differentiate the function

$$g(t)=\frac{7}{(2t-3)^2}.$$

Solution Begin by rewriting the function as

\(g(t)=-7(2t-3)^{-2}.\)

Apply the General Power Rule with \(u=2t-3\) produces

$${g}'(t)$$	$$=\color{red}{\underbrace{\color{black}{(-7)}}_{\color{red}{\text{Constant}\\ \text{Multiple}\\\text{ Rule}}}}\color{red}{\overbrace{\color{black}{(-2)}}^{\color{red}{n}}}\color{red}{\overbrace{\color{black}{(2t-3)}}^{\color{red}{ u^{n-1} }}}\color{red}{\overbrace{\color{black}{(2)}}^{\color{red}{ {u}' }}} $$	Apply General Power Rule
	\(28(2t-3)^{-3}\)	Simplify
	$$=\frac{28}{(2t-3)^3}.$$	Write with positive exponent

Simplifying Derivatives

Examples 2.4.7, 2.4.8, and 2.4.9 demonstrate techniques for simplifying functions with products, quotients, and composites.

Example 2.4.7 Simplifying by Factoring Out the Least Powers

Find the derivative for \(f(x)=x^2 \sqrt{1-x^2}.\)
Solution

Example 2.4.8 Simplifying the Derivative for a Quotient

Example 2.4.9 Simplifying the Derivative for a Power

Trigonometric Functions and the Chain Rule

The trigonometric functions below are expressed according to the Chain Rule

$$\frac{d}{dx}[\sin u]=(\cos u){u}'$$	$$\frac{d}{dx}[\cos u]=-(\sin u){u}'$$
$$\frac{d}{dx}[\tan u]=(\sec^2 u){u}'$$	$$\frac{d}{dx}[\cot u]=-(\csc^2 u){u}'$$
$$\frac{d}{dx}[\sec u]=(\sec u \tan u){u}'$$	$$\frac{d}{dx}[\sin u]=-(\csc u \cot ){u}'$$

Example 2.4.10 The Chain Rule and Trigonometric Functions

Example 2.4.11 Parentheses and Trigonometric Functions

To differentiate a function with the form \(k(x)=f(g(h(x)))\), apply the Chain Rule twice, as shown in Example 2.4.12.

Example 2.4.12 Applying the Chain Rule Repeatedly

Example 2.4.13 Tangent Line for a Trigonometric Function

Figure 2.4.3

Find an equation for the tangent line to the graph for (f(x)=2 \sin x + \cos 2x\)at the point \((\pi,1)\), as shown in Figure 2.4.3. Then determine all values for \(x\) on the interval \((0,2 \pi)\) at which the graph for \(f\) has a horizontal tangent. Solution Begin by finding \({f}'(x)\) \(f(x)\) \(=2 \sin x + \cos 2x\)     Write original function \({f}'(x)\) \(=2 \cos x+ (-\sin 2x)(2)\)     Apply Chain Rule to \(\cos 2x\) \(=2 \cos x -2 \sin 2x\)     Simplify Evaluate \({f}'(\pi)\) to find the tangent line at \((\pi,1)\). \({f}'(\pi)\) \(=2 \cos \color{red}{\pi} -2 \sin 2 \color{red}{\pi}\)     Substitute. \(=-2\)     Slope for graph at \((\pi,1)\). Express the equation in point-slope form. \(y-y_1\) \(=m(x-x_1)\)     Point-slope form \(y-\color{red}{1}\) \(=\color{red}{-2}(x-\color{\pi})\)     Substitute for \(y_1\), \(m\), and \(x_1\). \(y\) \(=1-2x+2\pi.\)     Equation for the tangent line at \((\pi,1)\) Conclude that \({f}'(x)=0\) when \(x=\frac{\pi}{6},\frac{\pi}{2},\frac{5\pi}{6},\text{ and }\frac{3\pi}{2}.\) Then \(f\) has horizontal tangents at \(x=\frac{\pi}{6},\frac{\pi}{2},\:\frac{5\pi}{6}, \text{ and }\frac{3\pi}{2}.\)

Internal Links

Parent Article: Calculus I 02 Differentiation