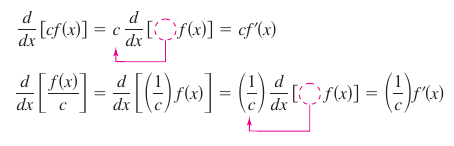Calculus I 02.02 Basic Differentiation Rules and Change Rate

Previous	Calculus I 02.01 The_Derivative and the Tangent Line Problem
Next	Calculus I 02.03 Product_Rule,_Quotient Rule, and Higher-Order Derivatives

Basic Differentiation Rules and Change Rate

• Find derivatives using the Constant, Constant Multiple, Power, and Sum and Difference Rules.
• Find derivatives for Change Rates

The Constant Rule

A derivative can be found by indirect means. One is the Constant Rule.

Theorem 2.2.1 The Constant Rule

The slope for a horizontal line is zero. Thus the relationship between a slope and derivative. Figure 2.2.1

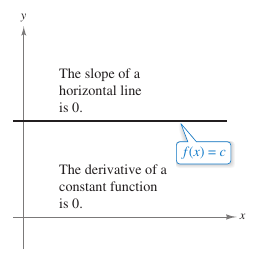
The derivative for a constant function is zero. That is, if \(c\) is a real number, then $$\frac{d}{dx}[c]=0$$, as shown in Figure 2.2.1. Proof Let \(f(x)=c\). Then apply the limit definition for the derivative. $$\frac{d}{dx}[c]$$ $$=\lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}$$ $$=\lim_{\Delta x \to 0}\frac{c-c}{\Delta x}$$ $$=\lim_{\Delta x \to 0}0$$ \(=0.\)

Example 2.2.1 Using the Constant Rule

Function	Derivative
a.\(y=7\)	\(dy/dx=0\)
b.\(f(x)=0\)	\({f}'(x)=0\)
c.\(s(x)= -3\)	\({s}'(t)=0\)
d.\(y=k\pi^2, \:k \text{ is a constant}\)	\({y}'=0\)

The Simple Power Rule

Consider the procedure for expanding a binomial.

\((x+\Delta x)^2=x^2+2x\Delta x + (\Delta x)^2\)

\((x+\Delta x)^3=x^3+3x^2\Delta x + 3x(\Delta x)^2+(\Delta x)^3\)

\((x+\Delta x)^4=x^4+4x^3\Delta x + 6x^2(\Delta x)^2+4x(\Delta x)^3+(\Delta x)^4\)

\((x+\Delta x)^5=x^5+5x^4\Delta x + 10x^3(\Delta x)^2+10x^2(\Delta x)^3+5x(\Delta x)^4+(\Delta x)^5\)

The general binomial expansion for a positive integer \(n\) is

$$(x+\Delta x)^n=x^n+nx^{n-1}(\Delta x)+\color{red}{\underbrace{\color{black}{ \frac{n(n-1)x^{n-2}}{2}(\Delta x)^2+...+(\Delta x)^n. }}_{\color{red}{(\Delta x)^2\text{ is a factor for these terms.}}}} $$

This binomial expansion is used in proving a special case, The Power Rule.

Theorem 2.2.2 The Simple Power Rule

If \(n\) is a rational number, then the function \(f(x)=x^n\) is differentiable and

$$\frac{d}{dx}[x^n]=n x^{n-1}.$$

For \(f\) to be differentiable at \(x=0\), \(n\) must be a number such that \(x^{n-1}\) is defined on an interval containing zero.
Proof If \(n\) is a positive integer greater than one, then the binomial expansion produces

$$\frac{d}{dx}[x^n]$$	$$=\lim_{\Delta x \to 0}\frac{x^n+nx^{n-1}(\Delta x)+\frac{n(n-1)x^{n-2}}{2}(\Delta x)^2+...+(\Delta x)^n-x^n}{\Delta x}$$
	$$=\lim_{\Delta x \to 0} \left [ nx^{n-1}+\frac{n(n-1)x^{n-2}}{2}(\Delta x)+...+(\Delta x)^{n-1} \right ]$$
	\(=nx^{n-1}+0+...+0\)
	\(=nx^{n-1}.\)

This proves the case for which n is a positive integer greater than one. The case for \(n=1\) is left as an exercise. Example 2.3.7 proves the case for which \(n\) is a negative integer. In Section 5.5 the Power Rule is extended to irrational values for \(n\).

The slope for the line \(y=x\) is one. Figure 2.2.2

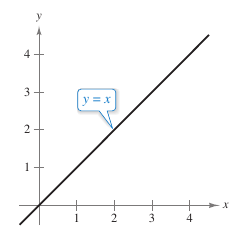
When using the Power Rule, the case for which \(n=1\) is a special case for the Power Rule. That is, $$\frac{d}{dx}[x]=1.$$     The Power Rule when \(n=1\) This rule is consistent with fact that the slope for the line \(y=x\) is one, as shown in Figure 2.2.2.

Example 2.2.2 Using the Power Rule

Function		Derivative
a.	\(f(x)=x^3\)	\({f}'(x)=3x^2\)
b.	\(g(x)=\sqrt[3]{x}\)	$${g}'(x)=\frac{d}{dx}[x^{1/3}]=\frac{1}{3}x^{-2/3}=\frac{1}{3x^{2/3}}$$
c.	$$y=\frac{1}{x^2}$$	$$\frac{dy}{dx}= \frac{d}{dx}[x^{-2}]=(-2)x^{-3}=-\frac{2}{x^3}$$

In Example 2.2.2(c), note that before differentiating, \(1/x^2\) was written as \(x^{-2}\). Rewriting is the first step in many differentiation problems.

Given:	Rewrite:	Differentiate:	Simplify:
$$y=\frac{1}{x^2}$$	$$y=x^{-2}\:\:\:\:$$	$$\frac{dy}{dx}=(-2)x^{-3}$$	$$\frac{dy}{dx}=-\frac{2}{x^3}$$

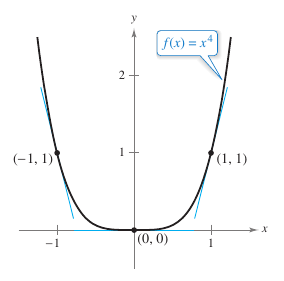
Example 2.2.3 Finding the Slope for a Graph

The slope is negative at \((-1,1)\),the slope is zero at \((0,0)\), and the slope is positive at \((1,1)\). Figure 2.2.3

Find the slope for the graph for \(f(x)=x^4\) for each value below. a.\(x=-1\)     b.\(x=0\)     c.\(x=1\) Solution The slope for a graph at a point is the derivative's value at that point. The derivative for \(f\) is \({f}'(x)=4x^3\). a. When \(x=-1\), the slope is \({f}'(\color{red}{-1})=4(\color{red}{-1})^3=-4.\)     Slope is negative b. When \(x=0\), the slope is \({f}'(\color{red}{0})=4(\color{red}{0})^3=-4.\)     Slope is zero c. When \(x=1\), the slope is \({f}'(\color{red}{1})=4(\color{red}{1})^3=-4.\)     Slope is positive This is shown in Figure 2.2.3.

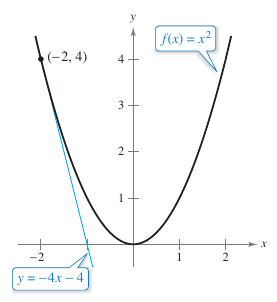
Example 2.2.4 Finding an Equation for a Tangent Line

The line \(y=-4x-4\) is tangent to the graph for \(f(x)=x^2\) at the point \((-2,4)\). Figure 2.2.4

Find an equation for the tangent line to the graph for \(f(x)=x^2\) when \(x=-2\). Solution To find the point on the graph for \(f\), evaluate the original function at \(x=-2\). \((-2,f(-2))=(-2,4)\)    Point on graph To find the slope when \(x=-2\) evaluate the derivative, \({f}'(x)=2x\), at \(x=-2\). \(m={f}'(-2)=-4\)    Slope from the graph at \((-2,4)\) Use the point-slope equation for a line and rewrite it as: \(y-y_1\) \(=m(x-x_1)\)     Point-slope form \(y-\color{red}{4}\) \(=\color{red}{-4}[x-(\color{red}{-2})]\)     Substitute for \(y_1,\:m,\: \text{ and }x_1\). \(y\) \(=-4x-4.\)     Simplify. as shown in Figure 2.2.4.

The Constant Multiple Rule

Theorem 2.2.3 The Constant Multiple Rule

If \(f\) is a differentiable function and \(c\) is a real number, then \(cf\)is also differentiable and

$$\frac{d}{dx}[cf(x)]=c{f}'(x).$$

Proof

$$\frac{d}{dx}[cf(x)]$$	$$= \lim_{\Delta x \to 0} \frac{cf(x+\Delta x)-cf(x)}{\Delta x}$$	Derivative Definition
	$$= \lim_{\Delta x \to 0}c \left [ \frac{f(x+\Delta x)-f(x)}{\Delta x} \right ]$$
	$$= c\left [ \lim_{\Delta x \to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} \right ]$$	Theorem 1.3.2
	\(=c{f}'(x)\)

The Constant Multiple Rule, simplified, states that constants can be factored from differentiation equation, as shown below

Example 2.2.5 Using the Constant Multiple Rule

Before differentiating functions involving radicals, rewrite the function with rational exponents.

Function		Derivative
a.	\(y=5x^3\)	$$\frac{dy}{dx}=\frac{d}{dx}[5x^3]=5\frac{d}{dx}[x^3]=5(3)x^2=15x^2$$
b.	$$y=\frac{2}{x}$$	$$\frac{dy}{dx}=\frac{d}{dx}[2x^{-1}]=2\frac{d}{dx}[x^{-1}]=2(-1)x^{-2}=-\frac{2}{x^2}$$
c.	$$f(t)=\frac{4t^2}{5}$$	$${f}'(t)= \frac{d}{dt}\left [ \frac{4}{5} t^2 \right ]=\frac{4}{5}(2t)=\frac{8}{5}t$$
d.	\(y=2\sqrt{x}\)	$$\frac{dy}{dx}=\frac{d}{dx} \left [ 2x^{1/2} \right ]= 2 \left ( \frac{1}{2} x^{-1/2} \right ) = \frac{1}{\sqrt{x}}$$
e.	$$y=\frac{1}{2\sqrt[3]{x^2}}$$	$$\frac{dy}{dx}=\frac{d}{dx} \left [ \frac{1}{2}x^{12/3} \right ]= \frac{1}{2} \left ( -\frac{2}{3} \right ) x^{-5/3}= -\frac{1}{3x^{5/3}}$$
f.	$$y=-\frac{3x}{2}$$	$${y}'=\frac{d}{dx} \left [ -\frac{3}{2}x \right ] = -\frac{3}{2}(1) = -\frac{3}{2}$$

The Constant Multiple and Power Rules can be combined into one.

$$\frac{d}{dx} [cx^n]=cnx^{n-1}.$$

Example 2.2.6 Using Parentheses When Differentiating

Original Function		Rewrite	Differentiate	Simplify
a.	$$y=\frac{5}{2x^3}$$	$$y=\frac{5}{2}(x^{-3})$$	$${y}'=\frac{5}{2}(-3x^{-4})$$	$${y}'=-\frac{15}{2x^4}$$
b.	$$y=\frac{5}{(2x)^3}$$	$$y=\frac{5}{8}(x^{-3})$$	$${y}'=\frac{5}{8}(-3x^{-4})$$	$${y}'=-\frac{15}{8x^4}$$
c.	$$y=\frac{7}{3x^{-2}}$$	$$y=\frac{7}{3}(x^2)$$	$${y}'=\frac{7}{3}(2x)$$	$${y}'=\frac{14x}{3}$$
d.	$$y=frac{7}{(3x)^{-2}}$$	\(y=63(x^2)\)	\({y}'=63(2x)\)	\({y}'=126x\)

The Sum and Difference Rules

Theorem 2.2.4 The Sum and Difference Rules

The sum or difference between two differentiable functions \(f\) and \(g\) is itself differentiable. In addition the derivative for \(f+g\) or \(f-g\) is the sum or difference between the derivatives for \(f\) and \(g\).

$$\frac{d}{dx}[f(x)+g(x)]={f}'(x)+{g}'(x)$$	Sum Rule
$$\frac{d}{dx}[f(x)-g(x)]={f}'(x)-{g}'(x)$$	Difference Rule

Proof The Sum Rule follows from Theorem 1.3.2. So does the Difference Rule.

$$\frac{d}{dx}[f(x)+g(x)]$$	$$=\lim_{\Delta x \to 0} \frac{ [f(x+\Delta x) +g(x+\Delta x)]-[f(x)+g(x)]}{\Delta x}$$
	$$=\lim_{\Delta x \to 0} \frac{ f(x+\Delta x) +g(x+\Delta x)-f(x)-g(x)}{\Delta x}$$
	$$=\lim_{\Delta x \to 0} \left [ \frac{ f(x+\Delta x)-f(x)}{\Delta x} +\frac{g(x+\Delta x)-g(x)}{\Delta x} \right ]$$
	$$=\lim_{\Delta x \to 0} \frac{ f(x+\Delta x)-f(x)}{\Delta x} +\lim_{\Delta x \to 0} \frac{g(x+\Delta x)-g(x)}{\Delta x} $$
	\({f}'(x)+{g}'(x)\)

The Sum and Difference Rules can be extended to any compound expression with a finite function count. For example, if

\(F(x)=f(x)+g(x)-h(x)\), then \({F}'(x)={f}'(x)+{g}'(x)-{h}'(x).\)

Example 2.2.7 Using the Sum and Difference Rules

Function		Derivative
a.	\(f(x)=x^3-4x+5\)	\({f}'(x)=3x^2-4\)
b.	$$g(x)=-\frac{x^4}{2}+3x^3-2x$$	\({g}'(x)=-2x^3+9x^2-2\)
c.	$$y=\frac{3x^2-x+1}{x}=3x-1+\frac{1}{x}\:\:\:\:$$	$${y}'=3-\frac{1}{x^2}=\frac{3x^2-1}{x^2}$$

Derivatives with Sine and Cosine Function

The derivative for the sine function is the cosine function. Figure 2.2.5

Section 1.3 described the limits $$\lim_{\Delta x \to 0} \frac{\sin \Delta x}{\Delta x}=1 \text{ and } \lim_{\Delta x \to 0} \frac{1-\cos \Delta x}{\Delta x}=0.$$ These limits can be used to prove differentiation rules for sine and cosine functions. Section 2.3 describes differentiation rules for the other four trigonometric functions. Theorem 2.2.5 Derivatives of Sine and Cosine Functions $$ \frac{d}{dx}[\sin x]= \cos x \:\:\:\: \frac{d}{dx}[\cos x]=-\sin x$$ Proof This proves the first rule. The second rule is proved in a similar manner. $$\frac{d}{dx}[\sin x]$$ $$=\lim_{\Delta x \to 0} \frac{\sin(x+\Delta x) - \sin x}{\Delta x} \:\:\:\: \color{red}{\text{ Derivative Definition}}$$ $$=\lim_{\Delta x \to 0} \frac{\sin x \cos x \Delta x + \cos x \sin \Delta x - \sin x}{\Delta x}$$ $$=\lim_{\Delta x \to 0} \frac{\cos x \sin x \Delta x -( \sin )(1 - \cos x)}{\Delta x}$$ $$=\lim_{\Delta x \to 0}\left [(\cos x) \left (\frac{\sin x \Delta x }{\Delta x}\right )- (\sin x) \left ( \frac{1- \cos \Delta x}{\Delta x} \right ) \right ]$$ $$=\cos x \left ( \lim_{\Delta x \to 0} \frac{\sin \Delta x}{\Delta x} \right ) - \sin x \left ( \lim_{\Delta x \to 0}\frac{1- \cos \Delta x}{\Delta x} \right )$$ \(=(\cos x )(1)-(\sin x)(0)\) \(=\cos x\) 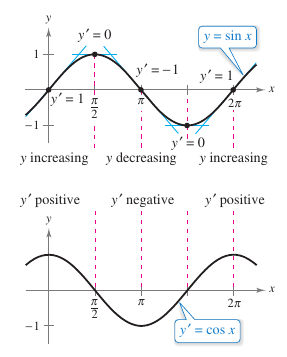Note that for each \(x\), the slope for the sine curve is equal to the value for cosine, as shown in Figure 2.2.5

Example 2.2.8 Derivatives Involving Sines and Cosines

$$\frac{d}{dx}[a \sin x]=a \cos x$$Figure 2.2.6

Function Derivative a. \(y=2 \sin x\) \({y}'=2 \cos x\) b. $$y=\frac{\sin x}{2}=\frac{1}{2} \sin x$$ $${y}'=\frac{1}{2} \cos x=\frac{\cos x}{2}$$ c. \(y=x+\cos x\) \({y}'=1- \sin x\) d. $$\cos x-\frac{\pi}{3} \sin x$$ $$-\sin x- \frac{\pi}{3}\cos x$$

Change Rate

The derivative can also be used to determine the change rate between two variables. Applications involving change rates, sometimes referred to as instantaneous change rate, occur in many fields. A few examples are population growth rates, production rates, water flow rates, velocity, and acceleration. A common use for change rates is to describe an object's motion moving in a straight line. It is customary to use either a horizontal or a vertical line with a designated origin to represent the motion. Movement to the right, or upward, is considered a positive direction, and movement to the left, or downward, is considered a negative direction.

The function \(s\) that gives the position, relative to the origin, for an object as a function with time \(t\) is called a position function. If, over a time period \(\Delta t\), the object changes its position by the amount

\(\Delta s=s(t+\Delta t)-s(t)\)

then, by the formula

$$\text{Rate}=\frac{\text{distance}}{\text{time}}$$

the average velocity is

$$\frac{\text{Change in distance}}{\text{Change in distance}}=\frac{\Delta s}{\Delta t}$$

Average velocity

Example 2.2.9 Finding Average Velocity for a Falling Object

Time-lapse photograph with a free-falling billiard ball. Figure 2.2.7

A billiard ball is dropped from a 100 foot height. The ball’s height \(s\) at time \(t\) is the position function \(s=-16t^2+100\)     Position function where \(s\) is measured in feet and \(t\) is measured in seconds. Find the average velocity over each time interval. a. \([1,2]\) b. \([1,1.5]\) c. \([1,1.1]\) Solution Note the average velocities are negative, indicating the object is moving downward.

The average velocity between \(t_1\) and \(t_2\) is the slope along the secant line. The instantaneous velocity at \(t_1\) is the slope on the tangent line. Figure 2.2.8

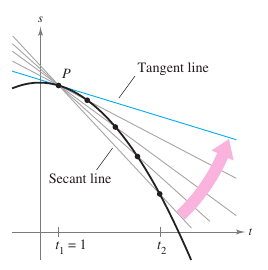
Suppose Example 2.2.9 was to find the instantaneous velocity, or simply the velocity, for the object when \(t=1\). Just as the slope for a tangent line is approximated by calculating the slope for the secant line, the velocity at \(t=1\) you can approximated by calculating the average velocity over a small interval, say, \([1,1+\Delta t]\), as shown in Figure 2.2.8. By taking the limit as \(\Delta t\) approaches zero the velocity when \(t=1\) is produced. Try doing this—you will find that the velocity when \(t=1\) is \(-32\) feet per second. In general, if \(s=s(t)\) is the position function for an object moving along a straight line, then the velocity for the object at time \(t\) is $$v(t)=\lim_{\Delta t \to 0} \frac{s(t+\Delta t)-s(t)}{\Delta t}={s}'(t).$$     Velocity function In other words, the velocity function is the derivative for the position function. Velocity can be negative, zero, or positive. An object's speed is the velocity's absolute value. Speed cannot be negative. The position for a free-falling object, neglecting air resistance, influenced by gravity can be represented by the equation $$v(t)= \frac{1)-s(t)}{2}gt^2 + v_0t+s_0$$     Position function where \(s_0\) is the object's initial height, \(v_0\) is the initial velocity, and \(g\) is the acceleration due to gravity. On Earth, the value for \(g\) is approximately \(-32\) feet per second per second or \(-9.8\) meters per second per second.

Example 2.2.10 Using the Derivative to Find Velocity

Velocity is positive when an object is rising, and is negative when it is falling. Notice that the diver moves upward for the first half-second because the velocity is positive for \(0 < t < 1/2\). When the velocity is zero, the diver's has reached the maximum height. Figure 2.2.9

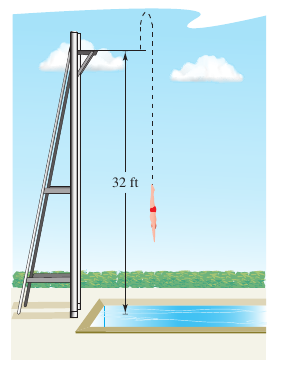
At time \(t=0\), a diver jumps from a platform diving board that is 32 feet above the water, as shown in Figure 2.2.9. Because the diver's initial velocity is 16 feet per second, the diver's position is \(s(t)=-16t^2+16t+32\)    Position function where \(s\) is measured in feet and \(t\) is measured in seconds. a. When does the diver hit the water? b. What is the diver's velocity at impact? Solution a. To find the time \(t\) when the diver hits the water, let \(s=0\) and solve for \(t\). \(-16t^2+16t+32\) \(=0\) Set position function equal to zero. \(16(t+1)(t-2)\) \(=0\)     Factor \(t\) \(=-1\text{ or }2\)     Solve for \(t\). Because \(t \leq 0\), choose the positive value to conclude the diver hits the water at \(t=2\) seconds. b. The velocity at time \(t\) is given by the derivative \({s}'(t)=-32t+16.\)     Velocity function Therefore, the velocity at time \(t=2\) is \({s}'(\color{red}{2})=-32(\color{red}{2})+ 16=-48\) feet per second

Internal Links

Parent Article: Calculus I 02 Differentiation