Calculus I 02.01 The Derivative and the Tangent Line Problem

Previous	Calculus I 01 Limits and Their Properties
Next	Calculus I 02.02 Basic Differentiation Rules and Change Rate

2.1 The Derivative and the Tangent Line Problem

• Find the slope for a tangent line to a curve at a point.
• Use the limit definition to find the derivative for a function.
• Understand the relationship between differentiability and continuity.

The Tangent Line Problem

Tangent line to a circle Figure 2.1.1

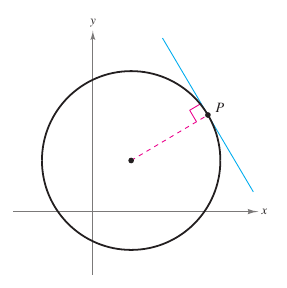
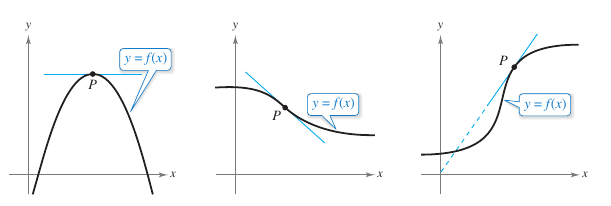
Calculus was created to solve four major problems that European mathematicians were working on during the seventeenth century. The tangent line problem (Section 1.1 and here) The velocity and acceleration problem ( Section 2.2 and Section 2.3) The minimum and maximum problem ( Section 3.1) The area problem (Section 1.1 and Section 4.2) The limit is in each problem. Therefore, calculus can be used to solve them. What does it mean that a line is tangent to a curve at a point? For a circle, the tangent line at a point \(P\) is the line that is perpendicular to the radial line at point \(P\), as shown in Figure 2.1.1. For a general curve the problem is more difficult. For example, how are the tangent lines defined in Figure 2.1.2? Say a line is tangent to a curve at a point \(P\) when it touches, but does not cross, the curve at point \(P\). This definition works for the first curve shown in Figure 2.1.2, but not for the second. A second definition might say a line is tangent to a curve when the line touches or intersects the curve at exactly one point. This definition would work for a circle, but not for more general curves, as the third curve in Figure 2.1.2 shows. Tangent line to a curve at a point Figure 2.1.2

The secant line through \((c,f(c))\) and \((c+\Delta x, f(c+\Delta x))\) Figure 2.1.3

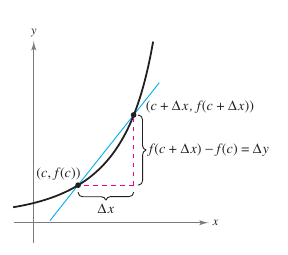
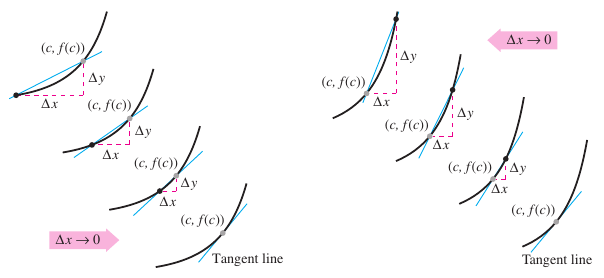
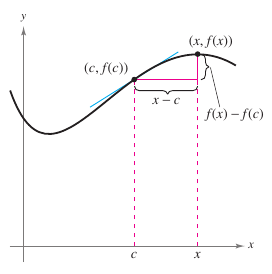
Finding the tangent line at a point \(P\) comes down to finding the slope for the tangent line at point \(P\). Approximate this slope using a secant line through the tangency point and a second point on the curve, as shown in Figure 2.1.3. If \((c,f(c))\) is the tangency point and \((c+\Delta x,f(c+ \Delta x))\) is a point on the graph for \(f\), then the secant line slope through the two points is given by substitution into the slope formula $$m$$ $$=\frac{y_2-y_1}{x_2-x_1}$$ $$m_{\sec}$$ $$= \frac{f(c+\Delta x)-f(c)}{(c+\Delta x) -c}$$ $$ \:\:\:\: \color{red}{\frac{\text{Change in}\:y}{\text{Change in }\:x}} $$ $$m_{\sec}$$ $$= \frac{f(c+\Delta x)-f(c)}{\Delta x}.$$     Secant line slop The right-hand side is a difference quotient. The denominator \(\Delta x\) is the change in \(x\), and the numerator \(\Delta y=f(c+\Delta x)-f(c)\) is the change in \(y\). Tangent line approximations Figure 2.1.4 Definition 2.1.1 Tangent Line with Slope \(m\) If \(f\) is defined on an open interval containing \(c\) and if the limit $$\lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x}=\lim_{\Delta x \to 0} \frac{f(c+ \Delta x)-f(c)}{\Delta x}=m$$ exists, then the line through \((c,f(c))\)with slope \(m\) is the tangent line to the graph for \(f\) at the point \((c,f(c))\).

Example 2.1.1 Finding the Slope for a Linear Function's Graph

The slope for \(f\) at \((2,1)\) is \(m=2\) Figure 2.1.5

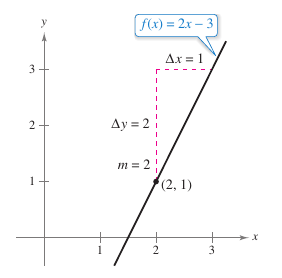
To find the slope on the graph for \(f(x)=2x-3\) when \(c=2\) apply the tangent line slope definition $$\lim_{\Delta x \to 0} \frac{f(2+ \Delta x)-f(2)}{\Delta x}$$ $$=\lim_{\Delta x \to 0} \frac{[(2+ \Delta x)-3]-[2(2)-3]}{\Delta x}$$ $$=\lim_{\Delta x \to 0} \frac{4+2\Delta x -3-4+3}{\Delta x}$$ $$\require{cancel} =\lim_{\Delta x \to 0} \frac{2\cancel{\Delta x}}{\cancel{\Delta x}}$$ $$=\lim_{\Delta x \to 0} 2 $$ \(=2\) The slope for \(f\) at \((c,f(c))=(2,1)\) is \(m=2\), as shown in Figure 2.1.5.

The graph for a linear function has the same slop at any point. This does not apply to nonlinear functions, as shown in Example 2.1.2.

Example 2.1.2 Tangent Lines for Nonlinear Function Graphs

The slope for \(f\) at any point \((c,f(c))\) is \(m=2c\) Figure 2.1.6

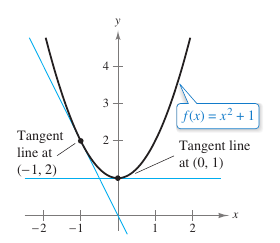
Find the slopes for the tangent lines to the graph for \(f(x)=x^2-1\) at the points \((0,1)\) and \((-1,2)\), as shown in Figure 2.1.6 Solution Let \((c,f(c))\) represent an arbitrary point on the graph for \(f\). Then the slope for the tangent line at \((c,f(c))\) can be found as shown below. Note that \(c\) is held constant as \(\Delta x\) approaches 0. $$\lim_{\Delta x \to 0} \frac{f(c+ \Delta x)-f(c)}{\Delta x}$$ $$=\lim_{\Delta x \to 0} \frac{[(c+ \Delta x)^2+1]-(c^2+1)}{\Delta x}$$ $$=\lim_{\Delta x \to 0} \frac{c^2+ 2c(\Delta x)+(\Delta x)^2+1-c^2-1}{\Delta x}$$ $$=\lim_{\Delta x \to 0} \frac{2(\Delta x)+(\Delta x)^2)}{\Delta x}$$ $$=\lim_{\Delta x \to 0} (2c+\Delta x)$$ \(=2c\) The slope at any point \((c,f(c))\) on the graph for \(f\) is \(m=2c\). At the point \((0,1)\), the slope is \(m=2(0)=0\), at the point \((-1,2)\), the slope is \(m=2(-1)=-2\).

Definition 2.1.2 Vertical Tangent Lines

The graph for \(f\) has a vertical tangent lin eat \((c,f(c))\) Figure 2.1.7

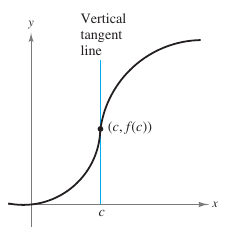
Definition 2.1.1 does not cover the case for a vertical tangent line. For vertical tangent lines use the following definition. If \(c\) is continuous at \(c\) and $$\lim_{\Delta x \to 0} \frac{f(c+ \Delta x)-f(c)}{\Delta x}= \infty$$ or $$\lim_{\Delta x \to 0} \frac{f(c+ \Delta x)-f(c)}{\Delta x}= -\infty$$ then the vertical line \(x=c\) passing through \((c,f(c))\) is a vertical tangent line to the graph for \(f\). For Example, the function shown in Figure 2.1.7 has a vertical tangent line at \((c,f(c))\). When the domain for \(f\) is the closed interval \([a,b]\) Definition 2.1.1 is extended to include endpoints by considering continuity and limits from the right (for \(x=a\)) and from the left (for \(x=b\)).

The Derivative for a Function

The discussion has reached a crucial point. Defining the Derivative. The limit used to define the tangent line slope is also used to define differentiation.

Definition 2.1.3 The Derivative for a Function

The derivative for \(f\) at \(x\) is

$${f}'(x)=\lim_{\Delta x \to 0} \frac{f(x+ \Delta x)-f(x)}{\Delta x}$$

provided the limit exists. For all \(x\) for which this limit exists, \({f}'\) is a function for \(x\). The notation \({f}'\) is read as "\(f\) prime of \(x\)".

The derivative for a function using \(x\) is also a function for \(x\). This new function produces the tangent line slope to the graph for \(f\) at the point \((x,f(x))\), provided the graph has a tangent line at that point. The derivative can also produce the instantaneous change rate for one variable with respect to another.

The procedure for finding the derivative is called differentiation. A function is differentiable at \(x\) when its derivative exists at \(x\) and is differentiable on an open interval \((a,b)\) when it is differentiable at every point in the interval.

Other notations used to denote the derivative for \(y=f(x)\) are below

$${f}'(x), \:\:\:\: \frac{dy}{dx},\:\:\:\: {y}',\:\:\:\:\frac{d}{dx}[f(x)],\:\:\:\:D_x[y].$$

Notation for derivatives

The notation \(dy/dx\) is read as "the derivative for \(y\) with respect to \(x\)" or simply "\(dy,dx\)". Adding limit notation they can be written as

$$\frac{dy}{dx}=\lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x}=\lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}={f}'(x).$$

Example 2.1.3 Finding the Derivative by the Limit Process

To find the derivative for \(f(x)=x^3+2x\) use the Derivative Definition, Definition 2.1.2.

$${f}'(x)$$	$$=\lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x} \:\:\:\: \color{red}{\text{Derivative definition}} $$
	$$=\lim_{\Delta x \to 0}\frac{(x+\Delta x)^3+2(x+\Delta x)-(x^3+2x)}{\Delta x}$$
	$$=\lim_{\Delta x \to 0}\frac{x^3+3x^2\Delta x +3x(\Delta x)^2+(\Delta x)^3+2x+2\Delta x-x^3-2x}{\Delta x}$$
	$$=\lim_{\Delta x \to 0}\frac{3x^2\Delta x+3x(\Delta x)^2+(\Delta x)^3+2\Delta x }{\Delta x}$$
	$$=\require{cancel}\lim_{\Delta x \to 0}\frac{\cancel{\Delta x}[3x^2+3x\Delta x+ (\Delta x)^2+2]}{\cancel{\Delta x}}$$
	$$=\lim_{\Delta x \to 0} [3x^2+3x\Delta x+ (\Delta x)^2+2]$$
	\(=3x^2+2\)

Example 2.1.4 Using the Derivative to Find the Slope at a Point

The slope for \(f\) at \((x,f(x)),\:x>0\), is \(m=1/(2 \sqrt{x})\). Figure 2.1.8

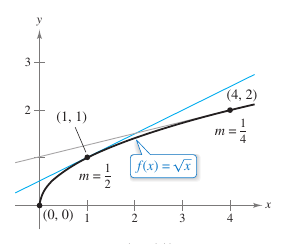
Find \({f}'\) for \(f(x)=\sqrt{x}\). Then find the slopes for the \(f\) graph at the points \((1,1)\) and \((4,2)\). Discuss \(f\)'s behavior at \((0,0)\). Solution Use the procedure for rationalizing numerators, as discussed in Section 1.3. $${f}'(x)$$ $$=\lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x} \:\:\:\: \color{red}{\text{Derivative definition}}$$ $$=\lim_{\Delta x \to 0}\frac{\sqrt{x+\Delta x}-\sqrt{x}}{\Delta x} $$ $$=\lim_{\Delta x \to 0} \left ( \frac{\sqrt{x+\Delta x}-\sqrt{x}}{\Delta x} \right ) \left ( \frac{\sqrt{x+\Delta x}-\sqrt{x}}{\sqrt{x+\Delta x}-\sqrt{x}} \right )$$ $$=\lim_{\Delta x \to 0}\frac{(x+\Delta x)-x}{\Delta x(\sqrt{x+\Delta x}+\sqrt{x})}$$ $$\require{cancel}=\lim_{\Delta x \to 0} \frac{\cancel{\Delta x}}{\cancel{\Delta x}(\sqrt{x+\Delta x}+\sqrt{x})}$$ $$=\lim_{\Delta x \to 0}\frac{1}{\sqrt{x+\Delta x}+\sqrt{x}}$$ $$=\frac{1}{2\sqrt{x}}, \:\:\:\: x>0$$ At the point \((1,1)\), the slope is \({f}'(1)=\frac{1}{2}\). At the point \((4,2)\), the slope is \({f}'(4)=\frac{1}{4}\). See Figure 2.1.8. At the point \((0,0)\), the slope is undefined. The graph for \(f\) has a vertical tangent line at \(0,0)\).

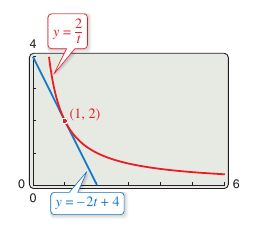
Example 2.1.5 Finding the Derivative for a Function

At the point \((1,2)\), the line \(y=-2t+4\) is tangent to the graph for \(y=2/t\). Figure 2.1.9

Find the derivative with respect to \(t\) for the function \(y=2/t\). Solution Consider \(y=f(t)\) and apply the Derivative definition to obtain $$\frac{dy}{dt}$$ $$=\lim_{\Delta t \to 0}\frac{f(t+\Delta t)-f(t)}{\Delta t}$$     Derivative definition $$=\lim_{\Delta t \to 0}\frac{\frac{2}{t+\Delta t}-\frac{2}{t}}{\Delta t} $$ $$\color{red} f(t+ \Delta t)=\frac{2}{t+\Delta t}\text{ and }f(t)=\frac{2}{t}$$ $$=\lim_{\Delta t \to 0} \frac{\frac{2t-2(t+\Delta t)}{t(t+\Delta t)}}{\Delta t} $$     Combine fractions in numerator. $$\require{cancel}=\lim_{\Delta t \to 0} \frac{-2\cancel{\Delta t}}{\cancel{\Delta t}(t)(t+\Delta t)}$$     Divide out the common factor \(\Delta t\). $$=\lim_{\Delta t \to 0} \frac{-2}{t(t+\Delta t)}$$     Simplify $$=-\frac{2}{t^2}$$     Evaluate limit as \(\Delta t \to 0\)

Differentiability and Continuity

As \(x\) approaches \(c\), the secant line approaches the tangent line. Figure 2.1.10

The alternative derivative limit form, shown below, is useful in investigating the relationship between differentiability and continuity. The derivative for \(f\) at \(c\) is $${f}'(c)=\lim_{x \to c} \frac{f(x)-f(c)}{x-c}$$     Derivative in alternative form. provided this limit exists, as shown in Figure 2.1.10. Note that for the limit in this alternative form to exist the one-sided limits $$\lim_{x \to c^-} \frac{f(x)-f(c)}{x-c}$$ and $$\lim_{x \to c^+} \frac{f(x)-f(c)}{x-c}$$ exist and are equal. These one-sided limits are called the derivatives from the left and derivatives from the right. If follows that \(f\) is differentiable on the closed inverval \([a,b]\) when it is differentiable on \((a,b)\) and when the derivative from the right at \(a\) and the derivative from the left at \(b\) both exist.

The greater integer function is not differentiable at \(x=0\) because it is not continuous at \(x=0\). Figure 2.1.11

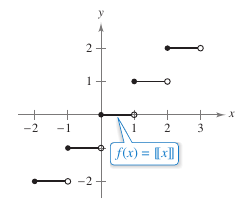
When a function is not continuous at \(x=c\), it is also not differentiable at \(x=c\). For instance, the greater integer function \(f(x)=[\![x]\!]\) is not continuous at \(x=0\). and is not differentiable at \(x=0\), as shown in Figure 2.1.11. This can be verified by observing that $$\lim_{x \to 0^-} \frac{f(x)-f(0)}{x-0}=\lim_{x \to 0^-} \frac{[\![x]\!]-0}{x} = \infty$$     Derivative from the left and $$\lim_{x \to 0^+} \frac{f(x)-f(0)}{x-0}=\lim_{x \to 0^+} \frac{[\![x]\!]-0}{x} = 0.$$     Derivative from the right While true that differentiability implies continuity, as shown in Theorem 2.1.1 below, the converse is not true. It is possible for a function to be continuous at \(x=c\) and not differentiable at \(x=c\). Examples 2.1.6 and 2.1.7 illustrate this possibility.

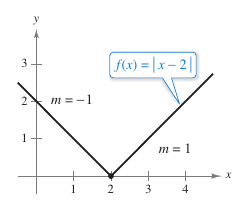
Example 2.1.6 A Graph with a Sharp Turn

\(f\) is not differentiable at \(x=2\) because the derivatives from the left and right are not equal. Figure 2.1.12

The function \(f(x)=|x-2|\), shown in Figure 2.1.12, is continuous at \(x=2\). The one-sided limits, however, $$\lim_{x \to 2^-} \frac{f(x)-f(2)}{x-2}=\lim_{x \to 2^-} \frac{|x-2|-0}{x-2} = -1$$     Derivative from the left and $$\lim_{x \to 2^+} \frac{f(x)-f(2)}{x-2}=\lim_{x \to 2^+} \frac{|x-2|-0}{x-2} = 0.$$     Derivative from the right are not equal. Therefore \(f\) is not differentiable at \(x=2\) and the graph for \(f\) does not have a tangent line at the point \((2,0)\).

Example 2.1.7 A Graph with a Vertical Tangent Line

\(f\) is not differentiable at \(x=2\) because \(f\) has a vertical tangent line at \(x=0\). Figure 2.1.13

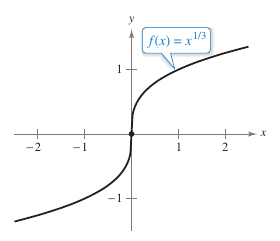
The function \(f(x)=x^{1/3}\) is continuous at \(x=0\), as shown in Figure 2.1.13. However, because the limit $$\lim_{x \to 0}\frac{f(x)-f(0)}{x-0}=\lim_{x \to 0}\frac{x^{1/3}-0}{x}=\lim_{x \to 0}\frac{1}{x^{\frac{2}{3}}}= \infty$$ is infinite, the conclusion is that the tangent line is vertical at \(x=0\). Therefore, \(f\) is not differentiable at \(x=0\).

Theorem 2.1.1 Differentiability Implies Continuity

If \(f\) is differentiable at \(x=c\), then \(f\) is continuous at \(x=c\).
Proof Prove that \(f\) is continuous at \(x=c\) by showing that \(f(x)\) approaches \(f(c)\) as \(x \to c\). To do this, use the differentiability for \(f\) at \(x=c\) and consider the following limit.

$$\lim_{x \to c}[f(x)-f(c)]$$	$$=\lim_{x \to c} \left [ (x-c) \left ( \frac{f(x)-f(c)}{x-c} \right ) \right ]$$
	$$= \left [ \lim_{x \to c} (x-c) \right ] \left [ \lim_{x \to c} \frac{f(x)-f(c)}{x-c}\right ]$$
	\(=(0)[{f}'(c)]\)
	\(=0\)

Because the difference \(f(x)-f(c)\) approaches zero as \(x \to c\), the conclusion is that \(\lim_{x \to c} f(x)=f(c)\). Therefore, \(f\) is continuous at \(x=c\).

Continuity and differentiability is summarized below.

1.	If a function is differentiable at \(x=c\), then it is continuous at \(x=c\). Therefore, differentiability implies continuity.
2.	It is possible for a function to be continuous at \(x=c\) and not be differentiable at \(x=c\). Therefore, continuity does not imply differentiability, as shown in Example 2.1.6.

Internal Links

Parent Article: Calculus I 02 Differentiation