Difference between revisions of "Calculus III 15.02 Line Integrals"
(→Definition 15.2.1 Line Integral) |
(No difference)
|
Latest revision as of 21:19, 15 October 2020
| Previous | Calculus III 15.01 Vector Fields |
| Next | Calculus III 15.03 Conservative Vector Fields and Independent Path |
Contents
- 1 15.2 Line Integrals
- 1.1 Piecewise Smooth Curves
- 1.2 Line Integrals[1]
- 1.2.1 Definition 15.2.1 Line Integral
- 1.2.2 Theorem 15.2.1 Evaluating a Line Integral as a Definite Integral
- 1.2.3 Example 15.2.2 Evaluating a Line Integral
- 1.2.4 Theorem 15.2.2 Line Integral Additive Property
- 1.2.5 Example 15.2.3 Evaluating a Line Integral Over a Path
- 1.2.6 Example 15.2.4 Evaluating a Line Integral
- 1.2.7 Example 15.2.5 Finding a Spring's Mass
- 1.3 Line Integrals for Vector Fields
- 1.4 Line Integrals in Differential Form
- 2 Internal Links
15.2 Line Integrals
- Understand and use a piecewise smooth curve.
- Write and evaluate a line integral.
- Write and evaluate a line integral for a vector field.
- Write and evaluate a line integral in differential form.
Piecewise Smooth Curves
Gravitational fields have a classic property that, subject to certain physical constraints, the work done by gravity on an object moving between two points in the field is independent from the object's path. One constraint is that the path must be a piecewise smooth curve. Recall that a plane curve \(C\) given by
- \(\textbf{r}(t)=x(t)\textbf{i}+y(t)\textbf{j}, \: a \leqslant t \leqslant b\)
is smooth when
- $$\frac{dx}{dt} \text{ and } \frac{dy}{dt}$$
are continuous on \([a,b]\) and not simultaneously 0 on \((a,b)\). Similarly, a three dimensional curve \(C\) given by
- \(\textbf{r}(t)=x(t)\textbf{i}+y(t)\textbf{j}+z(t)\textbf{k}, \: a \leqslant t \leqslant b\)
is smooth when
- $$\frac{dx}{dt}, \:\frac{dy}{dt}, \: \text{ and } \frac{dz}{dt}$$
are continuous on \([a,b]\) and not simultaneously 0 on \((a,b)\). A curve \(C\) is piecewise smooth when the interval \([a,b]\) can be partitioned into finite subintervals where on each \(C\) is smooth.
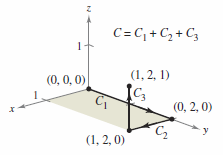
Example 15.2.1 Finding a Piecewise Smooth Parametrization
|
|
Find a piecewise smooth parametrization for \(C\)'s graph, as shown in Figure 15.2.1.
This produces \(C\) given by
Because \(C_{1}\), \(C_{2}\), and \(C_{3}\) are smooth, it follows that \(C\) is piecewise smooth. |
Recall that a curve's parametrization induces an orientation to the curve. For instance, in Example 15.2.1, the curve is oriented such that the positive direction is from \((0,0,0)\) to \((1,2,1)\).
Line Integrals[1]
|
|
An integral over a piecewise smooth curve \(C\)
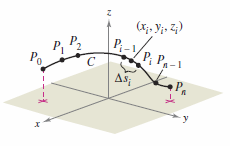
is called a line integral. (The terminology is somewhat unfortunate — this integral type might be better described as a “curve integral.”) Consider a wire mass with a finite length, given by a curve \(C\) in three dimensions. The density, mass per unit length, for the wire at the point \((x,y,z)\) is given by \(f(x,y,z)\). Partition the curve \(C\) by the points
produces \(n\) subarcs, as shown in Figure 15.2.2. The length for the \(i\)th subarc is given by \(\Delta S_{i}\). Choose a point \((x_{i},y_{i},z_{i})\) in each subarc. If each subarc has a small length, then the total wire mass can be approximated by the sum
By letting \(\| \Delta\|\) denote the longest subarc length and letting \(\| \Delta\|\) approach zero, it seems reasonable that this sum's limit approaches the wire's mass. This leads to Definition 15.2.1. |
Definition 15.2.1 Line Integral
If \(f\) is defined in a region containing a smooth curve \(C\) with a finite length, then the line integral for \(f\) along \(C\) is given by
|
Plane |
| or | |
|
Three dimensions |
provided this limit exists.
As with the integrals discussed in Chapter 14, evaluating a line integral is best accomplished by converting it to a definite integral. If \(f\) is continuous, then the limit given above exists and is the same for all smooth parametrizations for \(C\).
To evaluate a line integral over a plane curve \(C\) given by \(\textbf{r}(t)=x(t)\textbf{i}+y(t)\textbf{j}\), use the identity
|
Plane |
| or | |
|
Three dimensions |
If \(f\) is continuous, then the limit exists and is the same for all smooth parametrizations for \(C\).
Theorem 15.2.1 Evaluating a Line Integral as a Definite Integral
To evaluate a line integral over a plane curve \(C\) given by \(\textbf{r}(t)=x(t)\textbf{i}+y(t)\textbf{j}\), use the identity
- \(ds = \| \textbf{r}^{\prime}(t)\| \: dt = \sqrt{[x^{\prime}(t)]^{2}+y^{\prime}(t)]^{2}} \: dt.\)
Let \(f\) be continuous in a region containing a smooth curve \(C\). If \(C\) is given by \(\textbf{r}(t)=x(t)\textbf{i}+y(t)\textbf{j}\), where \(a \leqslant t \leqslant b\), then
- $$\int_{C} f(x,y) \: ds= \int_{a}^{b} f(x(t),y(t)) \sqrt{[x^{\prime}(t)]^{2}+y^{\prime}(t)]^{2}} \: dt.$$
If \(C\) is given by \(\textbf{r}(t)=x(t)\textbf{i}+y(t)\textbf{j}+z(t)\textbf{k}\), where \(a \leqslant t \leqslant b\), then
- $$\int_{C} f(x,y,z) \: ds= \int_{a}^{b} f(x(t),y(t),z(t)) \sqrt{[x^{\prime}(t)]^{2}+y^{\prime}(t)]^{2}+z^{\prime}(t)]^{2}} \: dt.$$
Note that if \(f(x,y,z)=1\), then the line integral gives the arc length for the curve \(C\), as defined in Section 12.5. That is,
- $$ \int_{C} 1 \: ds = \int_{a}^{b} \| \textbf{r}^{\prime}(t)\| \: dt = C \text{ curve length.}$$
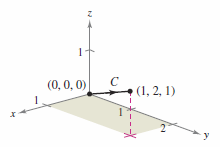
Example 15.2.2 Evaluating a Line Integral
|
|
Evaluate
where \(C\) is the line segment shown in Figure 15.2.3.
Therefore, \(x^{\prime}=1\), \(y^{\prime}=2\), and \(z^{\prime}=1\), which produces
Applying Theorem 15.2.1 produces
|
Theorem 15.2.2 Line Integral Additive Property
Let \(C\) be a path made from the smooth curves \(C_{1},C_{2},...,C_{n}\). If \(f\) is continuous on \(C\), then
- $$ \int_{C} f(x,y) \: ds = \int_{C_{1}} f(x,y) \: ds +\int_{C_{2}} f(x,y) \: ds + \cdot \cdot \cdot + \int_{C_{n}} f(x,y) \: ds .$$
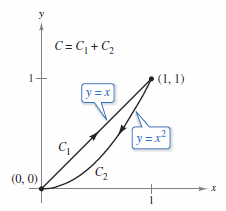
Example 15.2.3 Evaluating a Line Integral Over a Path
|
|
Evaluate
where \(C\) is the piecewise smooth curve shown in Figure 15.2.4.
For this curve,
which yields \(x^{\prime}(t)=1\) and \(y^{\prime}(t)=1\). Therefore,
back substitution produces
Next integrate down the parabola segment \(y=x^{2}\), using the following parametrization,
For this curve back substitution produces,
which yields \(x^{\prime}(t)=-1\) and \(y^{\prime}(t)=-2(1-t)\). Therefore,
back substitution produces
Applying Theorem 15.2.2 produces
|
Example 15.2.4 Evaluating a Line Integral
Evaluate
- $$ \int_{C} (x+2) \: ds,$$
where \(C\) is the curve represented by
- $$ \textbf{r}(t) = t\textbf{i}+\frac{4}{3}t^{3/2}\textbf{j}+\frac{1}{2}t^{2}\textbf{k}, \: 0 \leqslant t \leqslant 2.$$
Solution Because
- \(\textbf{r}^{\prime}(t) = \textbf{i}+2t^{1/2}\textbf{j}+t\textbf{k}\)
and
- \(\| \textbf{r}^{\prime}(t) \| = \sqrt{ [x^{\prime}(t)]^{2}+[y^{\prime}(t)]^{2}+[z^{\prime}(t)]^{2} }= \sqrt{1+4t+t^{2}}\)
it follows that
| $$\int_{C} (x+2) \: ds$$ | $$=\int_{0}^{2}(t+2)\sqrt{1+4t+t^{2}} \: dt $$ |
| $$=\frac{1}{2} \int_{0}^{2} 2(t+2)(1+4t+t^{2})^{1/2} \: dt $$ | |
| $$=\frac{1}{3} \left[ (1+4t+t^{2})^{3/2} \right]_{0}^{2} $$ | |
| $$=\frac{1}{3} (13 \sqrt{13}-1) \approx 15.29. $$ |
Example 15.2.5 Finding a Spring's Mass
|
|
Find the mass for a spring shaped as a circular helix
where \( 0 \leqslant t \leqslant 6 \pi\) and the spring's density is
as shown in Figure 15.2.5.
it follows that the spring's mass is
|
Line Integrals for Vector Fields
|
|
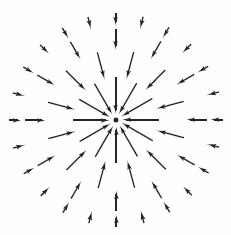
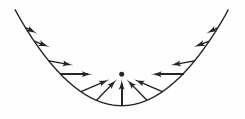
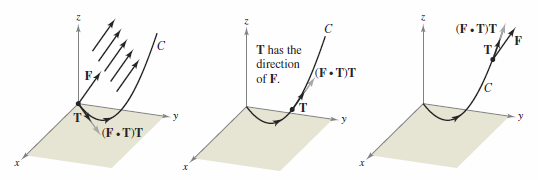
Line integrals can find the work done on an object moving in a force field. For example, Figure 15.2.6 shows an inverse square force field similar to the sun's gravitational field. Note the force magnitude along the circular path is constant, whereas the force magnitude along a parabolic path varies from point to point, as shown in Figure 15.2.7. Consider an object moving along a path \(C\) in the field, as shown in Figure 15.2.8. To determine the work done by the force, consider only the force that is acting in the same direction as the object, or the opposite direction. At each point on \(C\) the force \(\textbf{F}\) projects \(\textbf{F}\cdot \textbf{T}\) force onto the tangent vector \(\textbf{T}\). For each subarc with length \(\Delta S_{i}\), the incremental work is
where \((x_{i},y_{i},z_{i})\) is a point in the \(i\)th subarc. The total work done is given by the integral
|
Definition 15.2.2 Line Integral for a Vector Field
Let \(\textbf{F}\) be a continuous vector field defined on a smooth curve \(C\) given by
- \(\textbf{r}(t), \: a \leqslant t \leqslant b\).
The line integral for \(\textbf{F}\) on \(C\) is given by
| $$\int_{C} \textbf{F} \cdot d \textbf{r} $$ | $$=\int_{C} \textbf{F} \cdot \textbf{T} \: ds $$ |
| $$= \int_{a}^{b} \textbf{F} (x(t),y(t),z(t)) \cdot \textbf{r}^{\prime} \: dt.$$ |
Normalize \(\textbf{r}^{\prime}\) and substituting it into the definition produces
| $$\int \textbf{F} \cdot \textbf{T} \:ds $$ | $$=\int \textbf{F} \cdot \frac{\textbf{r}^{\prime}(t)}{\|\textbf{r}^{\prime}(t)\| } \|\textbf{r}^{\prime}(t) \| \:dt$$ |
| $$=\int \textbf{F} \cdot \textbf{r}^{\prime}(t) \: dt $$ | |
| $$=\int \textbf{F} \cdot d \textbf{r}.$$ |
Example 15.2.6 Work Done by a Force
|
|
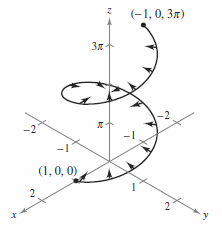
Find the work done by the force field
on a particle as it moves along the helix given by
from point \((1,0,0)\) to \((-1,0,3 \pi)\), as shown in Figure 15.2.9.
It follows that
The force field can be written as
To find the work done by the force field in moving a particle along the curve \(C\) use the identity
Then apply Definition 15.2.2.
Note the \(x\)- and \(y\)- variables contribute nothing to the total work. This occurs because in this particular example, the \(z\)- variable is the only one that is acting in the same, or opposite, direction to the particle's path, as shown in Figure 15.2.10. |
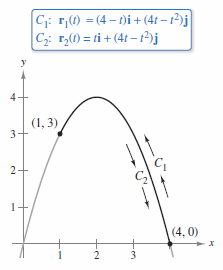
Example 15.2.7 Orientation and Parametrization for a Curve
|
|
Let
and evaluate the line integral
for each parabolic curve, as shown in Figure 15.2.11.
Solution If the curve's orientation is reversed, the unit tangent vector \(\textbf{T}(t)\) changes to \(-\textbf{T}(t)\), producing
|
Line Integrals in Differential Form
A second commonly used line integral form is derived from the vector field notation used in Section 15.1. If \(\textbf{F}\) is a vector field with the the form \(\textbf{F}(x,y)=M\textbf{i}+N\textbf{j}\), and \(C\) is given by \(\textbf{r}(t)= x(t)\textbf{i}+y(t)\textbf{j}\), the \(\textbf{F} \cdot d \textbf{r}\) is often written as \(M\: dx + N \: dy\).
| $$\int_{C} \textbf{F} \cdot \: d\textbf{r} $$ | $$=\int_{C} \textbf{F} \cdot \frac{ d\textbf{r}}{dt} \: dt $$ |
| $$=\int_{a}^{b} (M\textbf{i}+N\textbf{j}) \cdot (x^{\prime}(t)\textbf{i}+y^{\prime}(t)\textbf{j}) \: dt $$ | |
| $$=\int_{a}^{b} (M\frac{ dx}{dt}+N\frac{ dy}{dt}) \: dt $$ | |
| $$= \int_{C} (M \:dx + N \:dy )$$ |
This form can be extended to three variables.
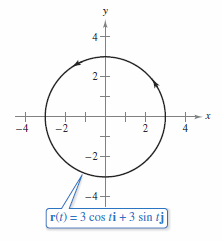
Example 15.2.8 Evaluating a Line Integral in Differential Form
|
|
Let \(C\) be a circle with radius 3 given by
as shown in Figure 15.2.12. Evaluate the integral
Solution Because \(x=3 \cos t\) and \(y=3 \sin t\) yields \(dx=-3\sin t \: dt\) and \(dy= 3 \cos t \: dt\). The line integral is
|
Curve \(C\)'s orientation changes the line integral's differential form. Consider if \(-C\) has an orientation opposite to \(C\), then
- $$ \int_{-C} M\: dx + N \: dy = - \int_{C} M\: dx + N \: dy.$$
For the three line integral forms discussed so far, \(C\)'s orientation does not affect the form \(\int_{C} f(x,y)\:ds\), but it does affect the vector and differential forms. For curves represented by \(y=g(x), \: a \leqslant x \leqslant b\), let \(x=t\) and obtain the parametric form
- \(x=t\) and \(y=g(x)\), \(a \leqslant x \leqslant b\).
Because \(dx=dt\) for this form the line integral can be evaluated with the variables \(x\) or \(t\). As demonstrated in Example 15.2.9.
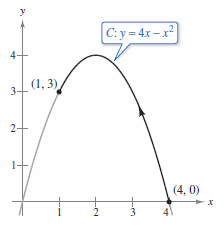
Example 15.2.9 Evaluating a Line Integral in Differential Form
|
|
Evaluate
where \(C\) is the parabolic arc given by \(y=4x-x^{2}\) from \((4,0)\) to \((1,3)\), as shown in Figure 15.2.13.
This produces a line integral
|
Internal Links
Parent Article: Calculus III 15 Vector Analysis