Calculus I 03.02 Rolle’s Theorem and the Mean Value Theorem

Previous	Calculus I 03.01 Extrema on an Interval
Next	Calculus I 03.03 Increasing and Decreasing Functions and the First Derivative Test

3.2 Rolle’s Theorem and the Mean Value Theorem

• Understand and use Rolle’s Theorem.
• Understand and use the Mean Value Theorem.

Rolle's Theorem [1]

The Extreme Value Theorem states that a continuous function on a closed interval \([a,b]\) must have both a minimum and a maximum on that interval. Both values, however, can occur at the endpoints. Rolle’s Theorem, named after the French mathematician Michel Rolle (1652–1719), gives conditions that guarantee an extreme value exists in the closed interval's interior.

Theorem 3.2.1 Rolle's Theorem

Let \(f\) be continuous on the closed interval \([a,b]\) and differentiable on the open interval \((a,b)\). If \(f(a)=f(b)\), then there is at least one number \(c\) in \((a,b)\) such that \({f}'(c)=0\).
Proof Let \(f(a)=d=f(b)\).
Case 1: If \(f(x)=d\) for all \(x\) in \([a,b]\), then \(f\) is constant on the interval and, by Theorem 2.2.1, \({f}'(x)=0\) for all \(x\) in \((a,b)\).
Case 2: Consider \(f(x)>d\) for some \(x\) in \((a,b)\). By the Extreme Value Theorem \(f\) has a maximum at some \(c\) in the interval. Because \(f(c)>d\), this maximum does not occur at either endpoint. Therefore, \(f\) has a maximum in the open interval \((a,b)\). This implies that \(f(c)\) is a relative maximum and, by Theorem 3.1.2, \(c\) is a critical number for \(f\). Because \(f\) is differentiable at \(c\) then \({f}'(c)=0\).
Case 3: When \(f(x)>d\) for some \(x\) in \((a,b)\), the argument in Case 2 applies but involving minimum and not maximum.

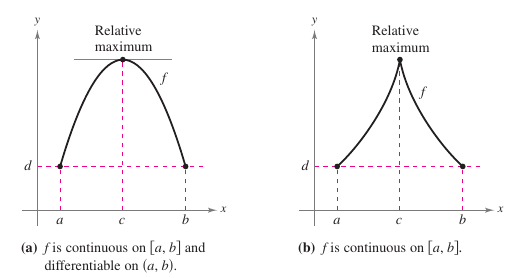
From Rolle’s Theorem, if a function \(f\) is continuous on \([a,b]\) and differentiable on \((a,b)\), and if \(f(a)=f(b)\), then there must be at least one \(x\)-value between \(a\) and \(b\) at which the graph for \(f\) has a horizontal tangent, as shown in Figure 3.2.1(a).When the differentiability requirement is dropped from Rolle’s Theorem, \(f\) will still have a critical number in \((a,b)\), but it may not yield a horizontal tangent. Such a case is shown in Figure 3.2.1(b).

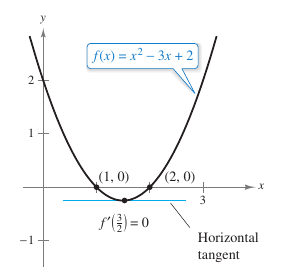
Example 3.2.1 Illustrating Rolle’s Theorem

The \(x\)-value for which \({f}'(x)=0\) is between two \(x\)-intercepts. Figure 3.2.2

Find the two \(x\)-intercepts for \(f(x)=x^2-3x+2\) and show that \({f}'(x)=0\) at some point between the two \(x\)-intercepts. Solution Note that \(f\) is differentiable on the entire real number line. Setting \(f(x)\) equal to zero produces \(x^2-3x+2 \) \(=0\)     Set \(f(x)\) equal to zero. \((x-1)(x-2)\) \(=0\)     Factor. \(x\) \(=1,\: 2\)     \(x\)-value for which \({f}'(x)=0\) Therefore, \(f(1)=f(2)=0\), and from Rolle's Theorem there exists at least one \(c\) in the interval \((1,2)\) such that \({f}'(c)=0\). To find such a \(c\), differentiate \(f\) to obtain \({f}'(x)=2x-3\)     Differentiate and then determine that \({f}'(x)=0\) when \(x=\frac{3}{2}\). Note that \(x\)-value lies in the open interval \((1,2)\), as shown in Figure 3.2.2.

Rolle’s Theorem states that when \(f\) satisfies the conditions for the theorem, there must be at least one point between \(a\) and \(b\) at which the derivative is zero. There may be more than one such point, as shown in Example 3.2.2.

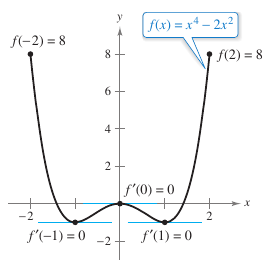
Example 3.2.2 Illustrating Rolle’s Theorem with Multiple \(x\) Values

\({f}'(x)=0\) for more than one \(x\)-value in the interval \((-2,2)\). Figure 3.2.3

Let \(f(x)=x^4-2x^2\). Find all values for \(c\) in the interval \((-2,2)\) such that \({f}'(c)=0\). Solution Not the function satisfies the conditions for Rolle's Theorem since \(f\) is differentiable on the interval \([-2,2]\) and differentiable on the interval \((-2,2)\). Because \(f(-2)=f(2)=8\) there exists at least one \(c\) in \((-2,2)\) such that \({f}'(c)=0\). Because \({f}'(x)=4x^3-4x\)     Differentiate setting the derivative equal to zero produces \(4x^3-4x\) \(=0\)     Set \({f}'(x)\) equal to zero. \(4x(x-1)(x+1)\) \(=0\)     Factor \(x\) \(=0,\:1,\:-1.\)     \(x\)-values for which \({f}'(x)=0\) On the interval \((-2,2)\) the derivative is zero at three different values for \(x\), as shown in Figure 3.2.3

The Mean Value Theorem

Figure 3.2.4

Rolle’s Theorem can be used to prove another theorem—the Mean Value Theorem. Theorem 3.2.2 The Mean Value Theorem If \(f\) is continuous on the closed interval \([a,b]\) and differentiable on the open interval \((a,b)\), then there exists a number \(c\) in \((a,b)\) such that $${f}'(c)=\frac{f(b)-f(a)}{b-a}.$$ The mean in the Mean Value Theorem refers to the mean, or average, change rate for \(f\) on the interval \([a,b]\). Proof Refer to Figure 3.2.4. The equation for the secant line that passes through the points \((a,f(a))\) and \((b,f(b))\) is $$y = \left [ \frac{f(b)-f(a)}{b-a} \right ] (x-a) + f(a).$$ Let \(g(x)\) be the difference between \(f(x)\) and \(y\). Then \(g(x)\) \(=f(x)-y\) $$=f(x)-\left [ \frac{f(b)-f(a)}{b-a} \right ] (x-a) - f(a).$$ Evaluating at \(g\) at \(a\) and \(b\) produces \(g(a)=0=g(b).\) Because \(f\) is continuous on \([a,b]\), it follows that \(g\) is also continuous on \([a,b]\). Because \(f\) is differentiable, \(g\) is also differentiable. Apply Rolle's Theorem to the function \(g\) proves that there exists a number \(c\) such that \({g}'(c)=0\), which implies that \({g}'(c)\) \(=0\) $${f}'(c)-\frac{f(b)-f(a)}{b-a} $$ \(=0.\) Therefore, there exists a number \(c\) in \((a,b)\) such that $${f}'(c)=\frac{f(b)-f(a)}{b-a}.$$

Although the Mean Value Theorem can be used directly in problem solving, it is used more often to prove other theorems. Some people consider this the most important theorem in calculus — it is closely related to the Fundamental Theorem of Calculus discussed in Section 4.4.

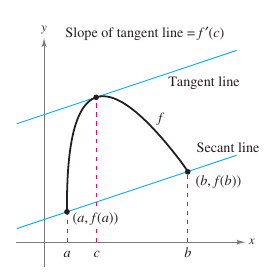
Geometrically, the theorem guarantees the existence for a tangent line that is parallel to the secant line through the points

\((a,f(a)) \text{ and } (b,f(b))\)

as shown in Figure 3.2.4. Example 3.2.3 illustrates this geometric interpretation for the Mean Value Theorem. In Change Rate terms, the Mean Value Theorem implies that there must be a point in the open interval \((a,b)\) at which the instantaneous change rate is equal to the average change rate over the interval \([a,b]\). This is illustrated in Example 3.2.4.

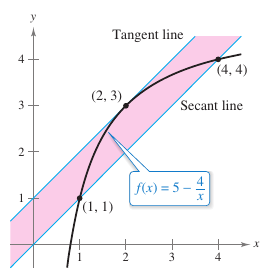
Example 3.2.3 Finding a Tangent Line

The tangent line at \((2,3)\) is parallel to the secant line through \((1,1)\) and \((4,4)\). Figure 3.2.5

For \(f(x)=5-(4/x),\) find all \(c\)-values in the open interval \((1,4)\)such that $${f}'(c)=\frac{f(4)-f(1)}{4-1}.$$ Solution The slope for the tangent line through \((1,f(1))\) and \((4,f(4))\) is $$\frac{f(4)-f(1)}{4-1}=\frac{4-1}{4-1}=1.$$     Slope for secant line. Note the function satisfies the Mean Value Theorem conditions. That is, \(f\) is continuous on the interval \([1,4]\) and differentiable on the interval \((1,4)\). Therefore, there exists at least one number \(c\) in \((1,4)\) such that \({f}'(c)=1\). Solving for \({f}'(c)=1\) yields $$\frac{4}{x^2}=1$$     Set \({f}'(x)\) equal to 1. which implies that \(x= \pm 2.\) On the interval \((1,4)\) the conclusion is that \(c=2\), as shown in Figure 3.2.4.

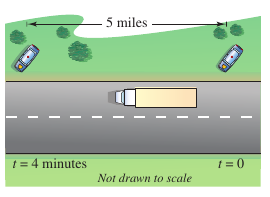
Example 3.2.4 Finding an Instantaneous Change Rate

At some time \(t\), the instantaneous velocity is equal to the average velocity over 4 minutes. Figure 3.2.6

Two stationary patrol cars equipped with radar are 5 miles apart on a highway, as shown in Figure 3.2.6. As a truck passes the first patrol car, its speed is clocked at 55 miles per hour. Four minutes later, when the truck passes the second patrol car, its speed is clocked at 50 miles per hour. Prove that the truck must have exceeded the 55 miles per hour speed limit at some time during the 4 minutes. Solution Let \(t=0\) be the time in hours when the truck passes the first patrol car. The time when the truck passes the second patrol car is $$t=\frac{4}{60}=\frac{1}{15} \text{ hour.}$$ By letting \(s(t)\) represent the distance in miles traveled by the truck yields \(s(0)=0\) and \(s(\frac{1}{15})=5.\) The average velocity for the truck over the five-mile highway stretch is $$\text{Average velocity }=\frac{s(1/15)-s(0)}{(1/15)-0}=\frac{5}{1/15}=75 \text{ miles per hour.}$$ Assuming the position function is differentiable, apply the Mean Value Theorem to conclude that the truck must have been traveling at 75 miles per hour sometime during the 4 minutes.

The Mean Value Theorem has a useful alternative form: If \(f\) is continuous on \([a,b]\) and differentiable on \((a,b)\), then there exists a number \(c\) in \((a,b)\) such that

\(f(b)=f(a)+(b-a){f}'(c).\)

Mean Value Theorem in alternative form.

Internal Links

Parent Article: Calculus I 03 Differentiation Applications