Calculus III 13.08 Extrema for Functions with Two Variables
| Previous | Calculus III 13.07 Tangent Planes and Normal Lines |
| Next | Calculus III 13.09 Extrema Applications |
Contents
13.8 Extrema for Functions with Two Variables
- Find absolute and relative extrema for a function with two variables.
- Use the Second Partials Test to find relative extrema for a function with two variables.
- Absolute Extrema
Relative Extrema
 \(R\) contains point(s) at which \(f(x,y)\) has a maximum and a minimum. Figure 13.8.1 |
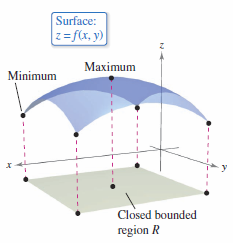
This discussion will extend Chapter 3's techniques for finding extreme values for a single variable function to functions with two variables. In Theorem 13.8.1 below, the Extreme Value Theorem for a function with one variable is extended to functions with two variables. Consider the continuous function \(f\) with two variables, defined on a closed bounded region \(R\). The values \(f(a,b)\) and \(f(c,d)\) such that
for all \((x,y)\) in \(R\) are called the maximum and minimum for \(f\) in the region \(R\), as shown in Figure 13.8.1. Recall from Section 13.2 that a region in the plane is closed when it contains all its boundary points. The Extreme Value Theorem deals with a region in the plane that is both closed and bounded. A region in the plane is bounded when it is inside a closed disk in the plane. Relative extrema and critical points can be extended to functions with three or more variables. When all first partial derivatives for
exists, it can shown that a relative maximum or minimum can occur at \(( x_{1},x_{2},x_{3},...,x_{n}) \) only when every first partial derivative is zero at that point. This means that critical points are obtained by solving the following equation system.
|
Theorem 13.8.1 Extreme Value Theorem
Let \(f\) be a continuous function with two variables \(x\) and \(y\) defined on a closed, bounded, region \(R\) in the \(xy\)-plane.
1. There is at least one point in \(R\) at which \(f\) takes on a maximum value.
2. There is at least one point in \(R\) at which \(f\) takes on a minimum value.
A maximum is also called an absolute maximum. A minimum is also called an absolute minimum. and As in single-variable calculus, there is a distinction made between absolute extrema and relative extrema.
Definition 13.8.1 Relative Extrema
 Relative extrema Figure 13.8.2 |
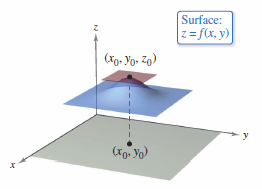
Let \(f\) be a function defined on a region \(R\) containing \((x_{0},y_{0})\).
for all \((x,y)\) in an open disk containing \((x_{0},y_{0})\).
for all \((x,y)\) in an open disk containing \((x_{0},y_{0})\). To say that \(f\) has a relative maximum at \((x_{0},y_{0})\) mean that the point \((x_{0},y_{0},z_{0})\) is at least as high as all nearby point on the graph for
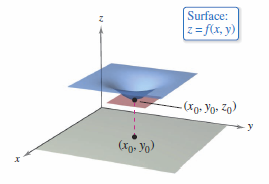
Similarly, \(f\) has a relative minimum at \((x_{0},y_{0})\) mean that the point \((x_{0},y_{0},z_{0})\) is at least as low as all nearby point on the graph, as shown in Figure 13.8.2. |
Definition 13.8.2 Critical Point
Let \(f\) be defined on an open region \(R\) containing \((x_{0},y_{0})\). The point \((x_{0},y_{0})\) is a critical point for \(f\) if either is true.
1. \(f_{x}(x_{0},y_{0}) = 0\) and \(f_{y}(x_{0},y_{0}) = 0\)
2. \(f_{x}(x_{0},y_{0}) \) or \(f_{y}(x_{0},y_{0}) \) does not exist.
The critical point for \(f\) is where the gradient is \(\textbf{0}\).
Recall from Theorem 13.6.3 that if \(f\) is differentiable and
- \( \nabla f(x_{0},y_{0}) = f_{x}(x_{0},y_{0})\textbf{i} + f_{y}(x_{0},y_{0})\textbf{j} = 0\textbf{i} + 0\textbf{j}\)
then every directional derivative at \((x_{0},y_{0})\) must be 0. This implies the function has a horizontal tangent plane at the point \((x_{0},y_{0})\), as shown in Figure 13.8.3, as the relative maximum, and in Figure 13.8.4, as the relative minimum.
 Relative maximum Figure 13.8.3 |
 Relative minimum Figure 13.8.4 |
Theorem 13.8.2 Relative Extremum Occur Only at Critical Points
If \(f\) has a relative extremum at \((x_{0},y_{0})\) on an open region \(R\), then \((x_{0},y_{0})\) is a critical point for \(f\).
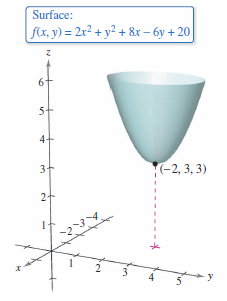
Example 13.8.1 Finding a Relative Extremum
 The function \(z=f(x,y)\) has a relative minimum at \((-2,3)\). Figure 13.8.5 |
Determine the relative extrema for
Solution Begin by finding the critical points for \(f\). Because
and
are defined for all \(x\) and \(y\), the only critical points are those for which both first partial derivatives are zero. To locate these points, set \( f_{x}(x,y) \) and \( f_{y}(x,y) \) equal to zero, and solve the equations
to obtain the critical point \((-2,3)\). Completing the square for \(f\) yields all \((x,y) \ne (-2,3)\)
Therefore, a relative minimum for \(f\) occurs at \((-2,3)\). The value for the relative minimum is \(f(-2,3)=3\), as shown in Figure 13.8.5. |
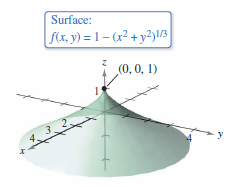
Example 13.8.2 Finding a Relative Extremum
 The functions \(f_{x}(x,y)\) and \(f_{y}(x,y)\) are undefined at \((0,0)\). Figure 13.8.6 |
Determine the relative extrema for
Solution Because
and
it follows that both partial derivatives exist for all point in the \(xy\)-plane except for \((0,0)\). Because the partial derivatives cannot both be zero unless both \(x\) and \(y\) are zero. Therefore, \((0,0)\) is the only critical point. The graph shows that \(f(0,0) = 1 \), as shown in Figure 13.8.6. For all other \((x,y)\)
Therefore, \(f\) has a relative maximum at \((0,0)\). The equation function \(f_{x}(x,y) = 0 \) for every point on the \(y\)-axis other than \((0,0)\). However, because \(f_{y}(x,y) \ne 0 \), these are not critical points. Remember that one partial must not exist or both must be zero to yield a critical point. |
The Second Partials Test
 Saddle point at \((0,0,0):f_{x}(0,0)=f_{y}(0,0)=0\). Figure 13.8.7 |
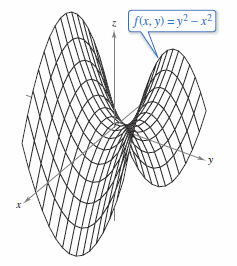
Theorem 13.8.2 states that finding relative extrema requires only examining values at critical points. Just as is with single variable functions, the critical points for two variable functions do not always yield relative maxima or minima. Some critical points yield saddle points, which are neither relative maxima nor relative minima. Consider the hyperbolic saddle paraboloid
as shown in Figure 13.8.7. At the point \((0,0)\), both partial derivatives
are zero. The function \(f\) does not, however, have a relative extremum at this point because in any open disk centered at \((0,0)\), the function takes on both negative values, along the \(x\)-axis, and positive values, along the \(y\)-axis. Therefore, the point \((0,0,0)\) is a saddle point on the surface. For the functions in Examples 13.8.1 and 13.8.2, it was relatively easy to determine the relative extrema, because each function was either given, or able to be written, in completed square form. For more complicated functions, algebraic arguments are less convenient and it is better to rely on the analytic means presented in the following Second Partials Test. This is the two-variable counterpart to the Second Derivative Test for functions with one variable. |
Theorem 13.8.3 Second Partials Test
Let \(f\) have continuous second partial derivatives on an open region containing a point \((a,b)\) for which
- \( f_{x}(a,b)=0\) and \( f_{y}(a,b)=0.\)
To test \(f\) for relative extrema, consider the quantity
- \(d= f_{xx}(a,b)f_{yy}(a,b) - [f_{xy}(a,b)]^{2} \).
1. If \(d>0\) and \(f_{xx}(a,b)>0\), then \(f\) has a relative minimum at \((a,b)\).
2. If \(d>0\) and \(f_{xx}(a,b)<0\), then \(f\) has a relative maximum at \((a,b)\).
3. If \(d<0\), then \((a,b,f(a,b))\) is a saddle point.
4. The test is inconclusive if \(d=0\).
A convenient device for remembering the formula for \(d\) in the Second Partials Test is given by the \(2 \times 2\) determinant
- $$ d = \begin{vmatrix} f_{xx}(a,b) & f_{xy}(a,b)\\ f_{yx}(a,b)& f_{yy}(a,b)\end{vmatrix}$$
where \(f_{xy}(a,b) = f_{yx}(a,b)\) by Theorem 13.3.1.
The theorem can fail to find relative extrema in two ways.
5. If either first partial derivative does not exit.
6. If \(d= f_{xx}(a,b)f_{yy}(a,b) - [f_{xy}(a,b)]^{2} = 0 \).
This can be extended to functions with three or more variables.
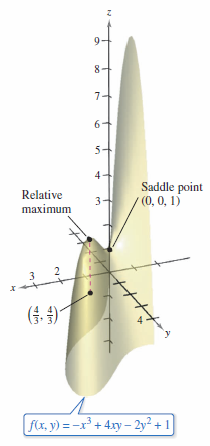
Example 13.8.3 Using the Second Partials Test
 Figure 13.8.8 |
Find the relative extrema for
Solution Begin by finding the critical points for \(f\). Because
exit for all \(x\) and \(y\), the only critical points are those for which both first partial derivatives are zero. To locate these points, set \( f_{x}(x,y) \) and \( f_{y}(x,y) \) equal to zero to obtain
The solutions are
it follows that, for the critical point \((0,0)\),
and, by the Second Partials Test, the saddle point is \((0,0,1)\) for \(f\).
and because \(f_{xx}(4/3,4/3) < 0\), \(f\) has a relative maximum at \((4/3,4/3)\), as shown in Figure 13.8.8. |
Example 13.8.4 The Second Partials Test Fails
 Figure 13.8.9 |
Find the relative extrema for
Solution Because
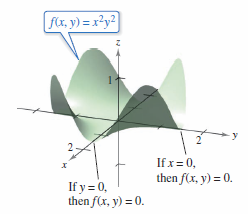
both partial derivatives are zero when \(x=0\) or \(y=0\). This means every point along the \(x\)- or \(y\)-axis is a critical point. Because
The Second Partials Test produces
which is zero when either \(x=0\) or \(y=0\). Therefore, the Second Partials Test fails. However, because \(f(x,y)=0\) for every point along the \(x\)- or \(y\)-axis and \(f(x,y)=x^{2}y^{2} > 0 \) for all other points, the conclusion is that these critical points yields an absolute minimum, as shown in Figure 13.8.9. |
Absolute Extrema
Absolute extrema for a function can occur in two ways. First, some relative extrema also happen to be absolute extrema. For instance, in Example 13.8.1, \(f(-2,3)\) is an absolute minimum for the function. The relative maximum found in Example 13.8.3 is not an absolute maximum for the function. Second, absolute extrema can occur at a boundary point on the domain. This is described in Example 13.8.5.
Example 13.8.5 The Second Partials Test Fails
 Figure 13.8.10 |
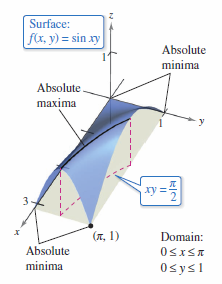
Find the absolute extrema for the function
on the closed region given by
Solution From the partial derivatives
each point lying on the hyperbola \(xy = \pi/2\) is a critical point. These points each yield the value
which is the absolute maximum, as shown in Figure 13.8.10. The only other critical point for \(f \) lying in the given region is \((0,0)\). It yields an absolute minimum value zero, because
implies that
To locate other absolute extrema, consider the four boundaries for the region formed by taking traces with the vertical planes \(x = 0\), \(x =\pi\), \( y =0\), and \(y = 1\). This yields \( \sin xy = 0\) at all points on the \(x\)-axis, at all points on the \(y\)-axis, and at the point \((\pi,1)\). Each point yields an absolute minimum for the surface, as shown in Figure 13.8.10. |
Internal Links
Parent Article: Calculus III 13 Functions with Several Variables
